导航
数据结构
算法
注:下文代码使用C++,以结构体数组实现
Amortized Analysis均摊分析
Aggregate Analysis
- 个操作总最差用时 , 则 amortized cost 为
Accounting method
- 类似存款存入不会比取出少,设计每种操作的均摊成本 ,当某次操作的 差额被称为 credit ,后面如果存在 的情况,差额可以用 credit 补上,则
Potential method
定义势能函数 ,则前文的 credit 就演化为
需要的复杂度不高于 ,方便起见可以让
作业题
T1:概念辨析
When doing amortized analysis, which one of the following statements is FALSE? A.Aggregate analysis shows that for all n, a sequence of n operations takes worst-case time T(n) in total. Then the amortized cost per operation is therefore T(n)/n B.For potential method, a good potential function should always assume its maximum at the start of the sequence C.For accounting method, when an operation's amortized cost exceeds its actual cost, we save the difference as credit to pay for later operations whose amortized cost is less than their actual cost D.The difference between aggregate analysis and accounting method is that the later one assumes that the amortized costs of the operations may differ from each other Answer : B
T2:势能函数设计

Answer : D

AVL Trees
定义:
- 空树是平衡的
- 非空树是平衡的当且仅当左右子树是平衡的且其高度差不超过1
注:定义空树高度为-1
Balance Factor:
- 没有绝对值,可以为负,对于平衡的树,BF取值为或
- 故当某节点的BF值不为上述值则需要调整
树高
- 记 为树高 h 的情况下节点数最小值,那么
- 与斐波那契对照,可得
- 从斐波那契数列的通项可以看出
结构体定义
struct Node{
int lson, rson, val, h;
}t[maxn];
Rotation Operations
- Left-Rotate
code
int Lrotate(int p){
int rs = t[p].rson;
t[p].rson = t[rs].lson;
t[rs].lson = p;
t[p].h = max(H(t[p].lson),H(t[p].rson))+1;
t[rs].h = max(H(t[rs].lson),H(t[rs].rson))+1;
return rs;
}
- Right-Rotate
code
int Rrotate(int p){
int ls = t[p].lson;
t[p].lson = t[ls].rson;
t[ls].rson = p;
t[p].h = max(H(t[p].lson),H(t[p].rson))+1;
t[ls].h = max(H(t[ls].lson),H(t[ls].rson))+1;
return ls;
}
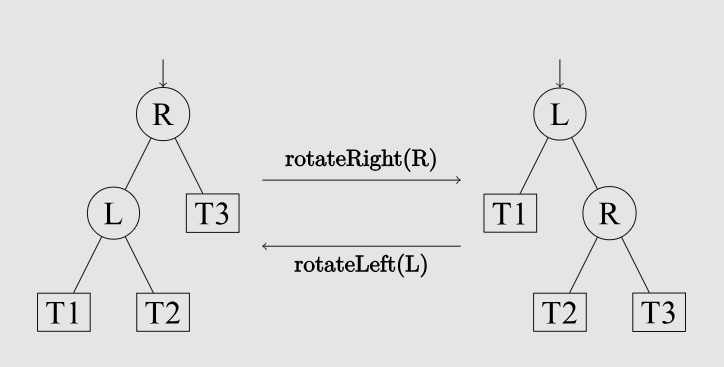
- LR-Rotate:先以 为中心左旋再以 为中心右旋
code
int LRrotate(int p){
t[p].lson = Lrotate(t[p].lson);
return Rrotate(p);
}
- RL-Rotate:先以 为中心右旋再以 为中心左旋
code
int RLrotate(int p){
t[p].rson = Rrotate(t[p].rson);
return Lrotate(p);
}
操作
Maintain
如果需要调整, ,以下以左倾为例进行分析(右倾是对称的)。树结构如下
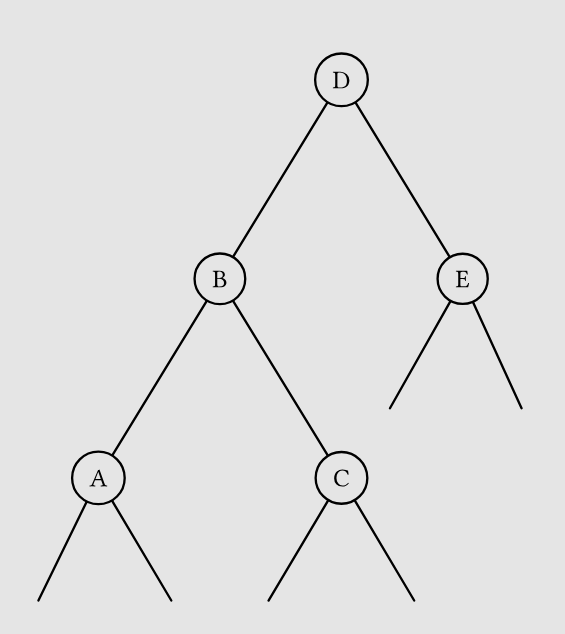
- 若 ,
Rrotate(D)即可
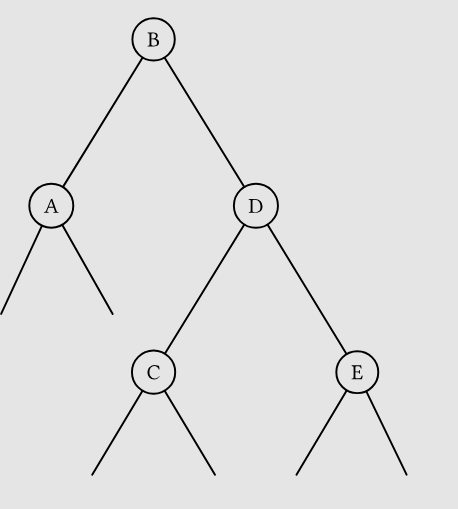
- 反之
LRrotate(D)
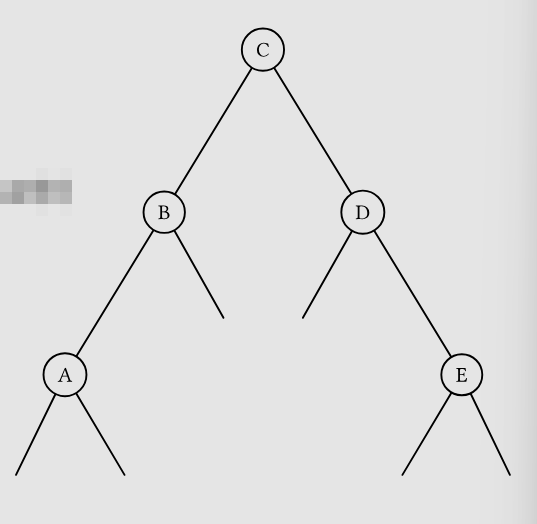
code
int H(int p){ return (p <= tot && p != 0)? t[p].h : -1; } void Maintain(int p){ int ls = t[p].lson, rs = t[p].rson; if(H(ls) - H(rs) == 2){ if(H(t[ls].lson) >= H(t[ls].rson)) Rrotate(p); else LRrotate(p); } else if(H(ls) - H(rs) == -2){ if(H(t[rs].rson) >= H(t[rs].lson)) Lrotate(p); else RLrotate(p); } t[p].h = max(H(t[p].lson),H(t[p].rson))+1; }- 显然复杂度
- 若 ,
Insert
- 因为要递归找到叶子所以是
- 只影响其祖先的BF值,故只用在递归的时候通过返回值提醒祖先节点进行检查。进一步观察可知,当某个节点通过Rotate完成调整后,该子树的 值相比插入前不变,故实际上只在离其最近的不平衡祖先进行调整
- 因为只在最近的不平衡祖先进行调整,而 Maintain 函数中最多进行一次 LR 或者 RL ,因此整个插入过程 Rotate 次数至多为 2
code
int insert(int p, int v){
if(!p){
t[++tot] = (Node){0, 0, v, 0};
return tot;
}
if(v <= t[p].val) t[p].lson = insert(t[p].lson,v);
else t[p].rson = insert(t[p].rson,v);
Maintain(p);
return p;
}
- Delete
- 删除节点
- 叶节点:直接删掉
- 只有左子树/右子树:用有的那个子节点替代自己(此时那个子节点一定是个叶节点)
- 兼有左右子树:取前驱/后继替代自己,将其节点删掉
- 从删除的叶节点向上调整即可
- 值得注意的是,删除节点后的向上调整并不停止于第一个失衡的祖先,一个节点删除可能引发上方处于BF值同号临界的一系列祖先都失衡需要旋转,因此旋转次数 ,总复杂度
- 删除节点
- Find, Predecessor, Successor, Rank:同正常二叉树,
作业题
T1:最少结点数计算
If the depth of an AVL tree is 6 (the depth of an empty tree is defined to be -1), then the minimum possible number of nodes in this tree is:33
T2:AVL的插入
Insert 2, 1, 4, 5, 9, 3, 6, 7 into an initially empty AVL tree. Which one of the following statements is FALSE? A.4 is the root B.3 and 7 are siblings C.2 and 6 are siblings D.9 is the parent of 7 Answer : B
Splay
一些名词
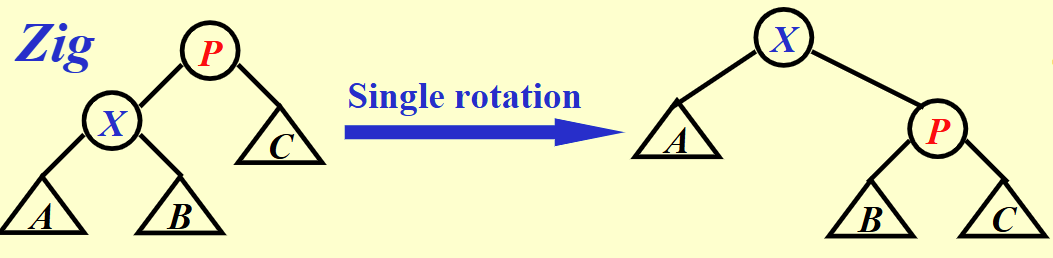
- zig : 当前节点向父节点位置旋转
- zig-zig : 自己&父节点&再上一级节点方向相同,对自己&父节点进行同向旋转
- zig-zag : 自己&父节点,父节点&再上一级节点方向不同,对自己进行两次反向旋转
(配图见下)
操作
Rotate
- 以右旋为例,设当前节点 , 父亲
- 的右儿子给 , 的左儿子给
- 若 有父亲 则 顶替 的位置
code
void Rotate(int x) { int y = fa[x], z = fa[y], chk = get(x); ch[y][chk] = ch[x][chk ^ 1]; if (ch[x][chk ^ 1]) fa[ch[x][chk ^ 1]] = y; ch[x][chk ^ 1] = y; fa[y] = x; fa[x] = z; if (z) ch[z][y == ch[z][1]] = x; maintain(y); maintain(x); }- 其中
maintain只是维护子树信息,由具体使用决定,一般是 , 因而整个操作
- 以右旋为例,设当前节点 , 父亲
Splay
- 核心操作,将一个节点一路转到根
code
bool get(int x) { return x == ch[fa[x]][1]; }
void Splay(int x) {
for (int f = fa[x]; f = fa[x], f; rotate(x))
if (fa[f]) Rotate(get(x) == get(f) ? f : x);
rt = x;
}
复杂度单次可能 ,但是均摊是 的,分析见下
Find
- 一路往下找 + splay上去
Delete
- 找到点并splay上去,如果计数为1则删除节点,否则合并两棵子树(查询当前根节点的前驱,将其设为根,并将其右儿子设为另一棵树的根)
code
void Delete(int k) {
Find(k);
if (cnt[rt] > 1) {
cnt[rt]--;
Maintain(rt);
return;
}
if (!ch[rt][0] && !ch[rt][1]) {
Clear(rt);
rt = 0;
return;
}
if (!ch[rt][0]) {
int cur = rt;
rt = ch[rt][1];
fa[rt] = 0;
Clear(cur);
return;
}
if (!ch[rt][1]) {
int cur = rt;
rt = ch[rt][0];
fa[rt] = 0;
Clear(cur);
return;
}
int cur = rt, x = Pre();
fa[ch[cur][1]] = x;
ch[x][1] = ch[cur][1];
Clear(cur);
Maintain(rt);
}
Insert操作
- 一路往下找+splay上去
Splay操作的复杂度分析
写完才发现oiwiki上有很详细的分析…挂个链接
势能函数,其中 指 的子树大小。记 ,则
zig, zig-zig, zig-zag本体复杂度为1,2,2
zig :
zig-zag:
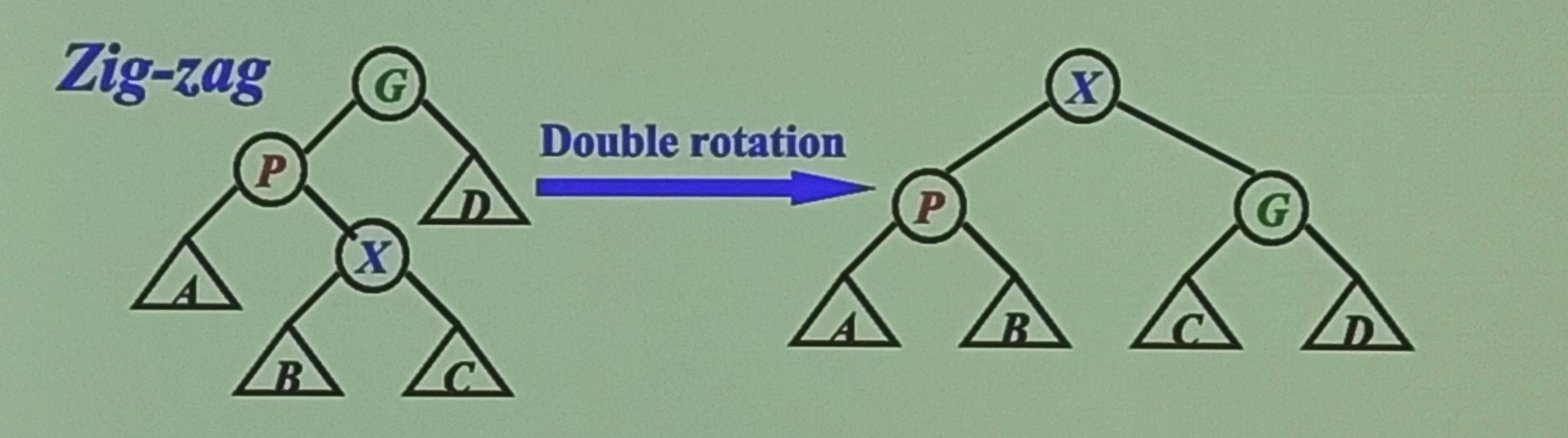
因为 故
又因为 , ,
令 , , , 则 , , 即
所以
zig-zig :
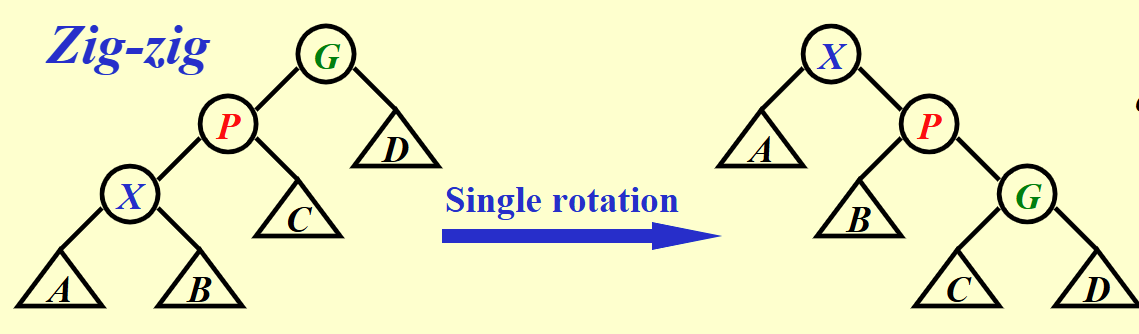
同理zig-zag的均值不等式可得 ,即
所以
假设一次splay共计进行了 步,因为单zig只会在转到根出现,则总复杂度
而 为 的,所以splay操作也是的
值得注意的是不一定为0
作业题
T1:access(splay)操作

Tips:与父亲同向则先转父亲,否则先转自己(然后都要转一次自己)
B+ Tree
是一种多叉树
定义 : A B+ tree of order M is a tree with following structural properties:
- Root: a leaf / has [2~M] children
- Nonleaf nodes (except root) : has [ , M] children
- Leaf: same depth
如图为 M = 3 的情况
可以看出非叶子节点最多存储 M-1 个键值,其中第 i 个对应其第 i+1 个子树中存储的最小值
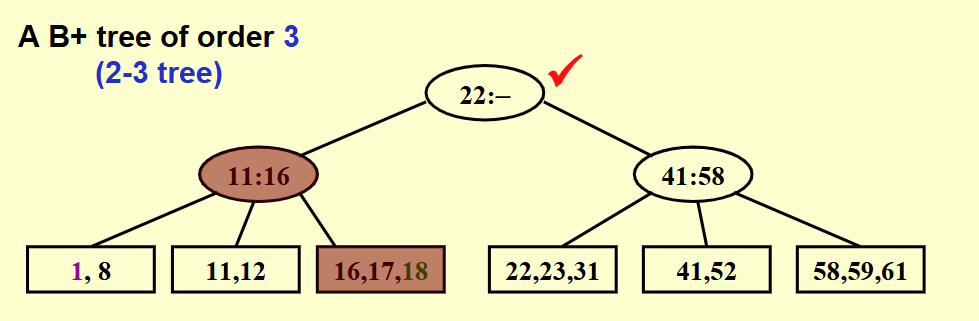
操作
- Find
- 与当前节点的所有子节点左边界值进行比较以找到应该在的区间
- 如果不使用二分查找优化复杂度 ,否则 。 Insert 和 Delete 操作同理。
code
Node Find(int key, Node cur){
int i = 0;
while( i < cur.cntSon )
if(key >= cur.keys[i] ) ++i;
if( i == cur.cntkeys ) return EmptyNode;
return Find(key, cur.son[i]);
}
- Insert
先递归到对应的区间,即叶节点,此时有几种情况
如果那个区间包含的数不超过 M - 1 个:直接插入进去就行
否则,需要对这个区间进行分裂,上层结构也需要有相应变化
- 当前叶节点分裂成两个,各自拥有 个数
- 递归处理父节点,直到找到一个儿子数量没到 的祖宗节点为止。如果直到根节点都不满足要求,重新建一0个根节点并将原根节点分裂
Check:检测是否已经存在
int Check(struct Node t, int v){
for(int i = t.totv; i; --i)
if(t.v[i - 1] == v) return 1;
return 0;
}
Set:更新节点属性
void Set(int id, int Totch, int Totv, int Leaf){
T[id].totch = Totch;
T[id].IsLeaf = Leaf;
T[id].totv = Totv;
}
UpdateRelation:更新节点亲子关系
void UpdateRelation(int ffa, int son0, int son1){
T[ffa].ch[0] = son0;
T[ffa].ch[1] = son1;
T[son0].fa = ffa;
T[son1].fa = ffa;
}
InsData:在指定数组插入数据并保持数组有序
void InsData(int *fro, int *dest, int *len, int val){
for(int i = 0; i < (*len); ++i){
dest[i] = fro[i];
}
dest[(*len)] = val;
for(int i = (*len); i && dest[i - 1] > val; --i){
dest[i] = dest[i - 1];
dest[i - 1] = val;
}
(*len)++;
}*
Deal:沿着链向上处理分裂
void deal(int cur, int son0, int son1, int insert_val){
if(!cur){
Set(cur = root = ++cnt, 2, 1, 0);
UpdateRelation(cur, son0, son1);
T[cur].v[0] = insert_val;
T[cur].fa = 0;
return;
}
//处理掉父亲关系问题
if(T[cur].totv < 2){
InsData(T[cur].v, T[cur].v, &T[cur].totv, insert_val);
int pos;
for(pos = T[cur].totch; pos; --pos){
if(T[cur].ch[pos - 1] == son0){
T[cur].ch[pos] = son1;
break;
}
T[cur].ch[pos] = T[cur].ch[pos - 1];
}
T[cur].totch++;
T[son1].fa = cur;
return;
}
// 分裂示意图
// / \(v2)
// cur(v1~v3) cur(v1) newnode(v3)
// / | \ => / \ / \
// A son B A son0 son1 B
//
InsData(T[cur].v, b, &T[cur].totv, insert_val);
Set(++cnt, 2, 1, 0);
T[cnt].v[0] = b[2];
Set(cur, 2, 1, 0);
T[cur].v[0] = b[0];
if(T[cur].ch[0] == son0) {
UpdateRelation(cnt, T[cur].ch[1], T[cur].ch[2]);
UpdateRelation(cur, son0, son1);
}
else if(T[cur].ch[1] == son0) {
UpdateRelation(cnt, son1, T[cur].ch[2]);
UpdateRelation(cur, T[cur].ch[0], son0);
}
else UpdateRelation(cnt, son0, son1);
deal(T[cur].fa, cur, cnt, b[1]);
}
Insert:插入值
int Insert(int cur, int val){
if(T[cur].IsLeaf){
if(Check(T[cur], val)) return 0;
if(T[cur].totv < 3){
InsData(T[cur].v, T[cur].v, &T[cur].totv, val);
}
else{
InsData(T[cur].v, b, &T[cur].totv, val);
Set(++cnt, 0, 2, 1);
Set(cur, 0, 2, 1);
for(int i = 0; i < 2; ++i){
T[cur].v[i] = b[i];
T[cnt].v[i] = b[2+i];
}
if(T[cur].fa)
deal(T[cur].fa, cur, cnt, b[2]);
else{
Set(root = ++cnt, 2, 1, 0);
T[root].v[0] = b[2];
T[root].fa = 0;
UpdateRelation(root, cur, cnt - 1);
}
}
return 1;
}
int to_node = 0;
for(int i = 0; i < T[cur].totv; ++i)
if(val >= T[cur].v[i]) ++to_node;
return Insert(T[cur].ch[to_node], val);
}
- Delete
- 同样是递归到相应叶节点进行处理
- 当删除掉当前值不会使叶节点包含值少于 ,直接删除
- 若删除后本节点不符合要求
- 若兄弟节点包含多于 个值,可以从兄弟节点借一个,并更新父节点中的分隔值
- 否则与兄弟节点合并并删除父节点中的分隔值,递归处理父节点
- 同样是递归到相应叶节点进行处理
作业题
T1:节点数计算
A 2-3 tree with 3 nonleaf nodes must have 18 keys at most.(T) Tips:叶节点指的是直接连向数值的节点而非数值本体
T2:插入与分裂操作
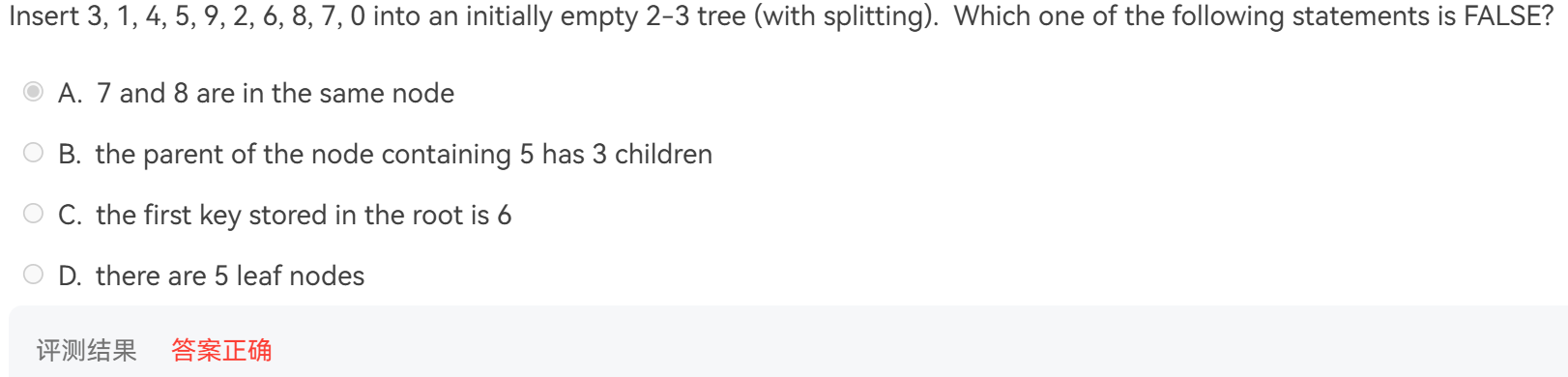
结构大致是(懒得画图,自行意会一下)
[6]
[2,4][8]
[0,1][2,3][4,5][6,7][8,9]
T3:删除操作
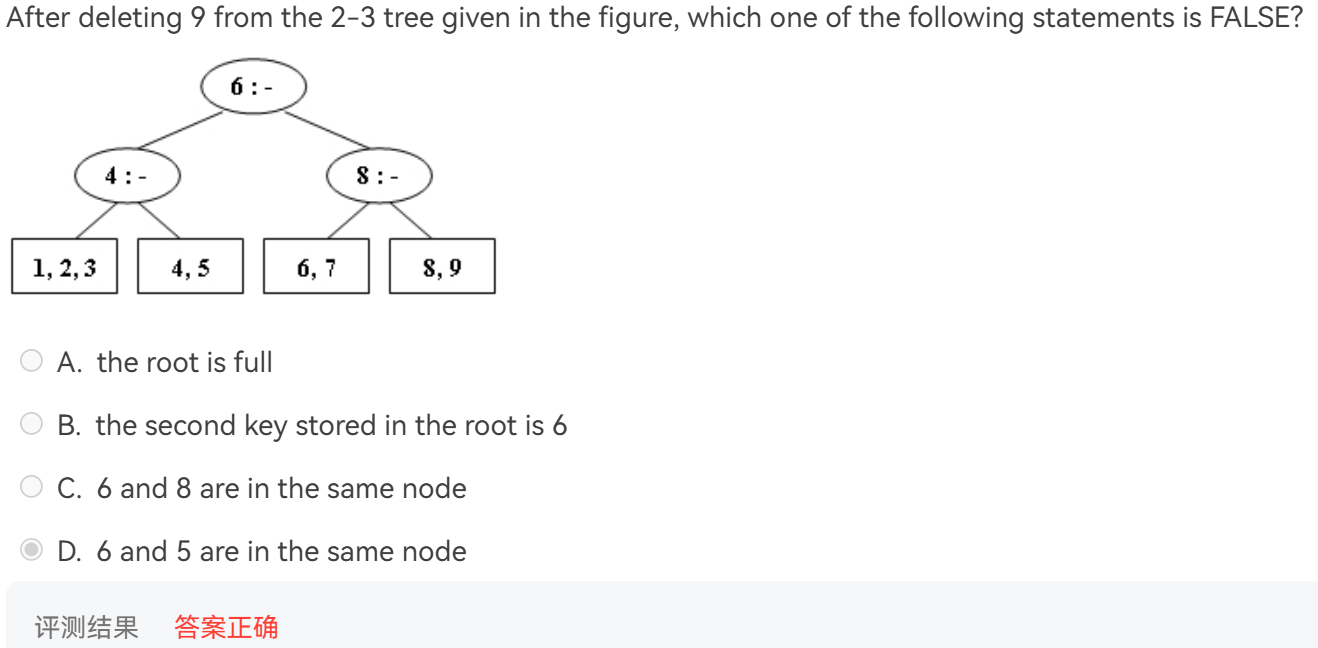
结构是
[4,6]
[1,2,3][4,5][6,7,8]
目前还没有写过删除的代码所以实现细节不明
T4:概念辨析

注意只有根节点这种特例!!
红黑树
定义: 一棵红黑树需要满足如下条件:
- 节点分为红黑两种颜色
- 根节点为黑色
- 空节点(NIL)为黑色
- 红色节点的子节点一定为黑色
- 从根节点往下到叶节点(NIL),每条路径上黑色节点数量相同
- 定义每个节点的黑高 (Black height)是从自己向下到NIL的路径上黑色节点的个数(但是不包含自己)
- 例如 BH(NIL) = 0, 单个节点的树 BH = 1(对应NIL,根节点本身不算在内)
- 定义每个节点的黑高 (Black height)是从自己向下到NIL的路径上黑色节点的个数(但是不包含自己)
性质:
可以得到的导出性质(用于判别红黑树):红黑树的红色节点的两个子节点一定同为叶子或同不为叶子(其中叶子指NIL)。
个内部节点(不含NIL)的红黑树的高度最大为
证明:综合以下两条
操作
Rotate : 与 AVL 的旋转操作基本一致
Insert
- 思路为先以红色节点的形式像普通BST一样插在叶节点(因为会有两个NIL所有肯定满足性质4,且插入红色节点不影响黑高),然后再调整使得红色节点不相邻。记插入节点为 x
若 x.fa 是黑色就不用调整
若 x.fa 是红色,需要分类讨论并且向上递归处理。下图中橘色节点代表使红黑树失衡的子树
case 1:将两个红色节点染黑,“根节点”染红,并向上递归处理(引号是因为是当前考虑的子树的根而不一定是整颗树的)
- 如果”根节点”没有父亲,则根节点再染黑,结束
- 如果”根节点“的父亲是黑,直接结束
- 如果根节点父亲是红的,向上递归,可能转成其他case
case 2 : 基于橙色节点左旋转为case 3
case 3 : 红色节点染黑,其父亲染红,再将新的黑色节点右旋上去
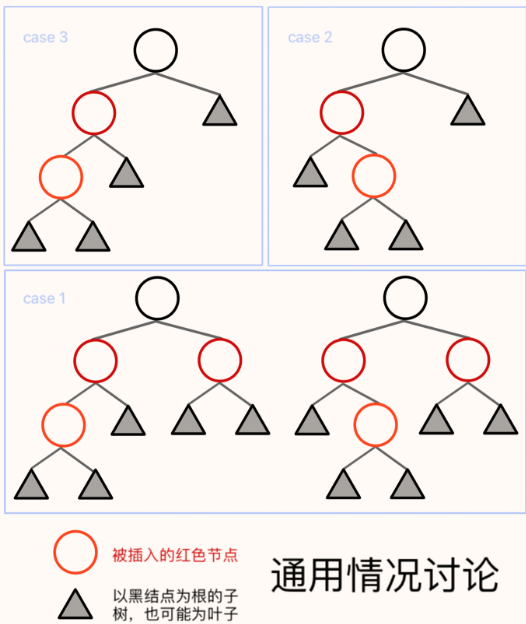
- 综合上述情况,只有case1可能向上递归,其他情况不会。只有case2 和 case3 需要 Rotate ,因此最多旋转次数为从 case2 转到 case3 ,即最多两次
复杂度
- 思路为先以红色节点的形式像普通BST一样插在叶节点(因为会有两个NIL所有肯定满足性质4,且插入红色节点不影响黑高),然后再调整使得红色节点不相邻。记插入节点为 x
Delete
赞美修佬考虑分成两部分进行分类讨论:删除和删除后平衡维护
删除
case 0 : 如果整颗树只有一个节点直接删,无需后续维护(可以理解为特化的 case 3 ? )
case 1 : 如果该节点左右儿子都有就取前驱/后继(只取值不取颜色)代替自己并删除前驱/后继对应节点,前驱/后继可能是没有儿子的,这种情况即转为 case 3 ,也可能是只有一个儿子的,这种情况即转为 case 2
case 2 : 如果该节点左右儿子只有一个,则那个节点一定是红的(因为黑高一致),则本节点一定是黑的。用子节点代替待删除节点并染黑即可,无需后续维护
case 3 : 如果该节点没有(非空)子节点,若节点为红直接删掉,节点为黑删掉后还要维护一下
结论 每个 case 都能转化为删除叶节点的情况,但只有在最后转化为删除某黑色节点时才会导致黑高的性质不能满足,需要进行平衡维护。
平衡维护:也需要递归地调整。记当前导致失衡的子树的根节点是x(颜色不定) ,依据兄弟节点(w)、其子节点(lc & rc)以及父亲节点(fa)进行分类。以下以 x 为左子树为例,右子树则需对称处理。
case 1 : w,lc,rc全黑
- case 1.1 fa 是红色的:将 w 染红, fa 染黑,相当于从 w 子树中抽一个黑色出来共享给 x
- case 1.2 fa 是黑色的:同样将 w 染红,然而在 fa 的子树内无法找到可以用来从红转黑共享给 x 的黑色节点,因而将矛盾转移到 fa 以上的部分。如果 fa 就是根节点,则可以直接退出(因为整棵树黑高平等减一)。
case 2 : w黑,rc红:将 w 染为和 fa 相同的颜色,将 rc 和 fa 染黑,并对 fa 进行一次左旋。思路是给 x 上方补一个黑节点,为了和其他子树保持一致顶上留一个与原 fa 相同的节点。因为 rc 的高度-1,将 rc 本身变黑以弥补。
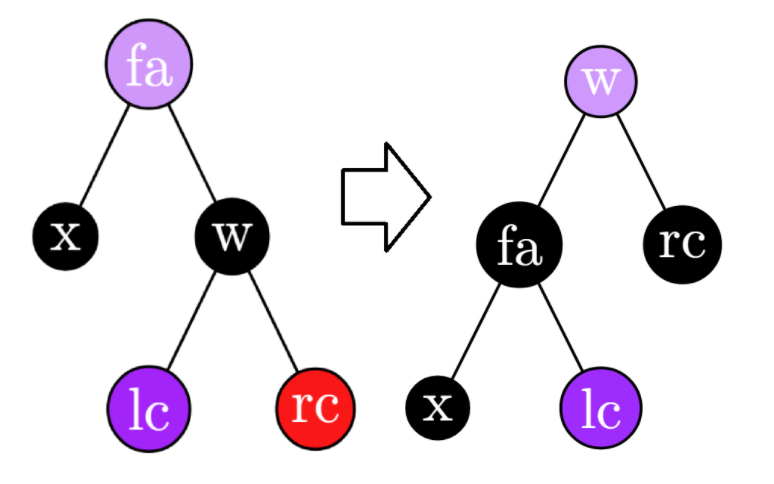
case 3 : w,rc黑,lc红:刚刚那个思路中更改 rc 颜色用于补偿的步骤无法实施。将 w 染红, lc 染黑,右旋 w 使得 b 成为新的根。可以发现在 w 和 lc 对调染色时, lc 的整体黑高比 rc 高了 1,其左右两子树的黑高倒是与 rc 一致,因此将 lc 转到根节点后 lc 子树内黑高与原先一致,但右子节点变红了,则状况转为 case 2 。
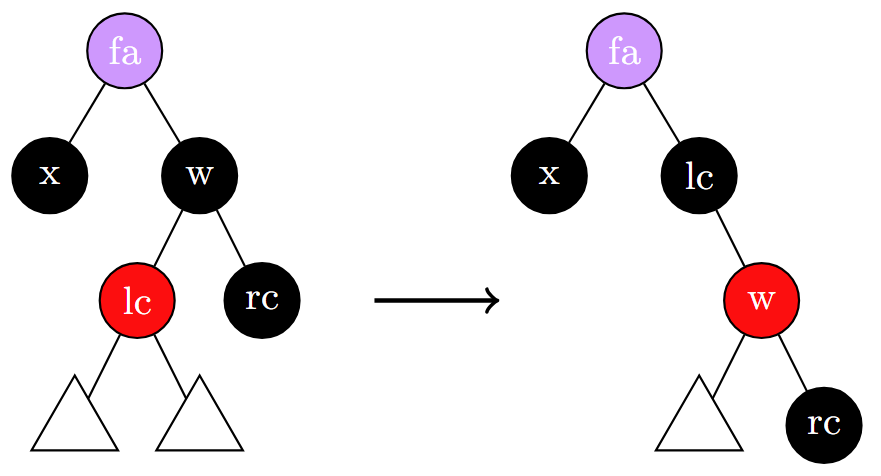
case 4 : fa,lc,rc黑,w红:将 fa 左旋,使 w 成为新的根节点。但此时左右两子树黑高差1,因此将 fa 染红, w 染黑(此时至少保证了向 lc 方向的路径与向 rc 方向的路径黑高一致),然而 fa 子树内黑高仍然不相等,因此递归到子树中去,可能转化为 case 1.1,case 2,case 3。
懒得画了,借一下oiwiki的图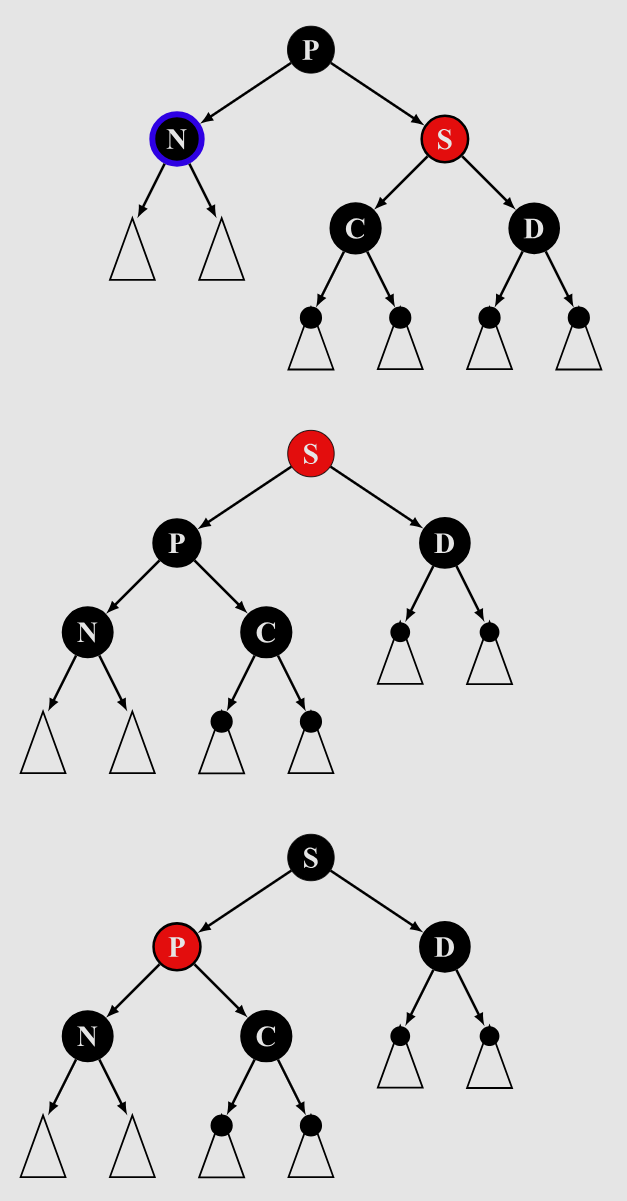
- 综合以上四种情况:case1.2需要向上递归,case4需要向下递归,剩余情况无需递归。case2,case3,case4中存在Rotate操作,则最多旋转次数为由 case4 转到 case3 再到 case2 ,共计3次
删除部分最坏即寻找前驱后继,复杂度为树高;平衡维护部分向上递归 (case1.2) 与向下递归 (case4) 不兼容,因此最坏复杂度即树高,
查找前驱后继等操作同正常 BST
比较:AVL与RBT的旋转操作次数
| AVL | RBT | |
|---|---|---|
| Insert | ||
| Delete |
作业题
T1:插入节点

Tips:得到结果19是红色的
T2:删除节点(但是强度很低)

Tips:谁顶上去谁变黑
Inverted File Index
定义:
- Index: a mechanism for locating a given term in a text.
- **Inverted file: ** contains a list of pointers (e.g. the number of a page) to all occurrences of that term in the text.
Word Stemming
- 将一个单词化为它的词根
Stop Words
- 可以理解为“虚词”,过于普遍的单词没必要 index (比如 a, the , it )
寻找单词
- Sol1 : Search trees(b tree,b+ tree, trie)
- Sol2 : Hashing
Distributed Indexing
- Term-partitioned Index 依据单词字典序存储,存储困难,检索容易,容灾能力差
- Document-partiitioned index 依据文章划分存储,存储容易,检索困难,容灾能力好
Dynamic Indexing
- 文档加入正常插入
- 文档删除:攒够一定量删除请求(存在auxiliary index)统一处理(写满了/定期),处理时需要在main index和auxiliary index同步检索
- 树型结构太大就改用懒删除
Thresholding
- Document:只取出权重前 x 的文档
- Query:对词组按出现频率排序,按照频率由高到低的词组搜索到的文档贡献不同的权重
Evaluate
对于一次搜索
| Relevant | Irrelevant | |
|---|---|---|
| Retrieved | ||
| Not Retrieved |
则有两个评估指标
- Precision精确度
- Recall召回率
作业题
T1:Distributed Indexing

区分两种存储方式
T2:Evaluation

问的是召回率
T3:accessing terms

哈希表不利于搜索序列和模糊搜索
左偏堆
- 思路:使右子树相对稀疏
- Npl : null path length,一个节点到其子树内没有两个孩子的节点的最短距离。特别的,Npl(NULL) = -1 。
- 左偏堆要求对于所有节点的左右儿子有
- 如果不满足可以交换左右儿子实现
- 性质
- 右路径长度为 r 的左偏堆至少拥有 个节点。(此时是满二叉树)[tips : 数学归纳法]
结构体定义
struct TreeNode{
ElementType Element;
PriorityQueue Left,Right;
int Npl;
};
复杂度
- Merge : O(logN)
code
PriorityQueue Merge( PriorityQueue H1, PriorityQueue H2 ) { if(H1 == NULL) return H2; if(H2 == NULL) return H1; if(H1->Element > H2->Element) swap(H1,H2); if(H1->Left == NULL) H1->Left = H2; else{ H1->Right = Merge(H1->Right,H2); if(H1->Left->Npl < H1->Right->Npl) SwapChildren(H1); H1->Npl = H1->Right->Npl + 1; } return H1; }- DeleteMin : 将根节点左右儿子合并就行,O(logN)
作业题
T1:Build heap

由这道题可以理解为什么左偏树和斜堆的BuildHeap复杂度是(斜堆是均摊)O(n)
斜堆
神必算法
- 每Merge必调换左右儿子
- 只有在合并的末尾,即叶子节点才无需交换左右儿子 ,这是与下面这份代码实现不同的
早年的代码一份
newnode(int v){//返回节点编号
int x=++cnt;
val[x]=v,ls[x]=rs[x]=0;
return x;
}
int merge(int a,int b){//以a,b为根的树合并,返回根节点
if(!a||!b) return a+b;
if(val[a] > val[b]) swap(a,b);
rs[a]=merge(rs[a],b);
swap(ls[a],rs[a]);
return a;
}
- 复杂度:均摊分析
- heavy nodes : 右子树大于左子树的节点
- 除了在归并路线上的节点,其他节点的轻重性质不变化
- 定义最开始的右路径(即归并路线)上轻节点 ,重节点 。
- 则 越多 越少( 多则堆趋于左倾堆,则右路径长度就短,至多到 级别)
- 极端情况变化:轻全变重
作业题
直接把结论列出来好了
- 按顺序插入 得到的总是完全满二叉树
- 斜堆的 right path 长度是任意的,只是轻节点数受到限制
二项队列
- 是一些堆(二项树)的集合(森林)
- k阶二项树( )由两个k-1阶二项树将两个根相连形成,特别的,单点是0阶。
- 共有 个节点,深度为 的一层(根为0)有 个
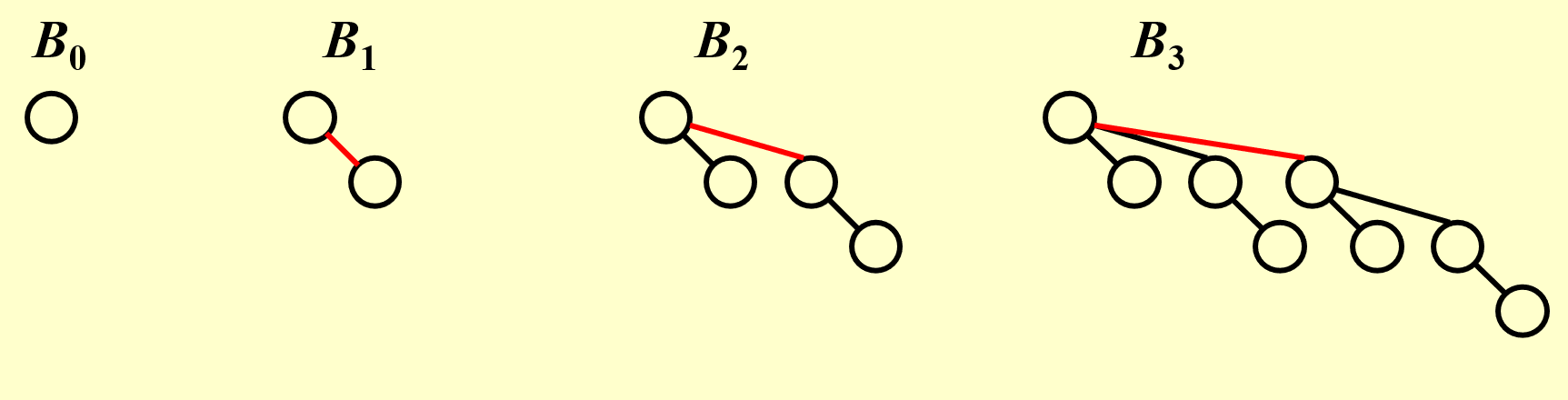
- 以长子兄弟的形式存储,同一节点的所有儿子按子树大小降序排列
操作
结构体定义
typedef struct BinNode *Position;
typedef struct Collection *BinQueue;
typedef struct BinNode *BinTree;
struct BinNode
{
ElementType Element;
Position LeftChild;
Position NextSibling;
};
struct Collection
{
int CurrentSize;
BinTree TheTrees[MaxTrees];
};
- Merge:单次复杂度 , 均摊
- 二项树的合并,显然 ,两个堆的合并类似于两个二进制数逐位做加法
两棵树的合并
BinTree CombineTrees( BinTree T1, BinTree T2 )
{
if(T1->Element > T2->Element) return CombineTrees(T2,T1);
T2->NextSibling = T1->LeftChild;
T1->LeftChild = T2;
return T1;
}
两个二项堆的合并
BinQueue Merge( BinQueue H1, BinQueue H2 )
{
BinTree T1,T2,Carry = NULL;
int i,j;
if( H1->CurrentSize + H2->CurrentSize > Capacity ) ErrorMessage();
H1->CurrentSize += H2->CurrentSize;
for( i = 0; j = 1; j <= H1->CurrentSize; ++i, j *= 2){
T1 = H1->TheTrees[i];
T2 = H2->TheTrees[i];
switch(4*!!Carry + 2*!!T2 + !!T1){
case 0:case 1:break;
case 2: H1->TheTrees[i] = T2;
H2->TheTrees[i] = NULL;break;
case 4: H1->TheTrees[i] = Carry;
Carry = NULL;break;
case 3: Carry = CombineTrees( T1, T2 );
H1->TheTrees[i] = H2->TheTrees[i] = NULL;break;
case 5: Carry = CombineTrees( T1, Carry );
H1->TheTrees[i] = NULL;break;
case 6: Carry = CombineTrees( T2, Carry );
H2->TheTrees[i] = NULL; break;
case 7: H1->TheTrees[i] = Carry;
Carry = CombineTrees( T1, T2 );
H2->TheTrees[i] = NULL; break;
}
}
return H1;
}
- Find-Min : 在根节点队列中遍历寻找 但是如果专门记录更新可以做到
- Insert:即将一棵 树合并到队列中,单次最好 最坏 , 均摊
- Build:将节点逐个插入,由均摊分析得总复杂度
- DeleteMin:将最小根节点取出,将其对应二项树拆成所有子树再Merge回去,
DeleteMin
ElementType DeleteMin( BinQueue H )
{
BinQueue DeletedQueue;
Position DeletedTree, OldRoot;
ElementType MinItem = Infinity;
int i, j, MinTree;
if ( IsEmpty( H ) ) { PrintErrorMessage(); return –Infinity; }
for ( i = 0; i < MaxTrees; i++) {
if( H->TheTrees[i] && H->TheTrees[i]->Element < MinItem ) {
MinItem = H->TheTrees[i]->Element; MinTree = i; }
} /* end for-i-loop */
DeletedTree = H->TheTrees[ MinTree ];
H->TheTrees[ MinTree ] = NULL;
OldRoot = DeletedTree;
DeletedTree = DeletedTree->LeftChild;
free(OldRoot);
DeletedQueue = Initialize();
DeletedQueue->CurrentSize = ( 1<= 0; j – – ) {
DeletedQueue->TheTrees[j] = DeletedTree;
DeletedTree = DeletedTree->NextSibling;
DeletedQueue->TheTrees[j]->NextSibling = NULL;
}
H->CurrentSize – = DeletedQueue->CurrentSize + 1;
H = Merge( H, DeletedQueue );
return MinItem;
}
- Decrease Key:在二叉树上进行上调,显然
均摊分析
建树
假设进行插入时现有单独的树,则插入时会与 到 合并得到一棵 ,其他不变,则 (正在插入的那个点也是一棵树)
为什么 ?
因为要有 次合并和 的创建节点
Banking Method : 每个点初始一块钱,合并操作花掉两棵子树之一(被合并成为儿子那个点)的一块钱,则整个树至少还有一块钱(在根节点上),则整个系统钱不会为负,因而总复杂度是 的
插入:由建树的过程可以得到每个点的插入平均下来是 的
总结:复杂度
| Heaps | Leftist | Skew | Binomial | Fibonacci | Binary | Link list |
|---|---|---|---|---|---|---|
| Make heap | ||||||
| Build heap | amortized | |||||
| Find-Min | 或 | |||||
| Merge(Union) | amortized | |||||
| Insert | amortized | amortized | ||||
| Delete-Min | amortized | amortized | ||||
| Decrease-Key | amortized | amortized |
注 :
- Make heap指初始化一个空的堆, Build heap则是依据已有数据构建堆
- Delete指在只知道数值的情况下删除数值对应节点
- Decrease-Key指将一已知节点的值修改并调整数据结构的过程
- Link list指无序的链表,仅用作对照
- 内容参考了Wikipedia
- 二项堆的Find-Min操作的两种复杂度取决于有没有用变量实时更新记录Min值,老师PPT中貌似默认不维护
| BST | RBTree | AVL | Splay | |
|---|---|---|---|---|
| Insert | amortized | |||
| Delete | amortized | |||
| Find | amortized |
Backtracking
回溯模板
bool Backtracking ( int i ){
Found = false;
if ( i > N )return true; /* solved with (x1, ..., xN) */
for ( each xi in Si ) {
/* check if satisfies the restriction R */
OK = Check((x1, ..., xi) , R );
/* pruning */
if ( OK ) {
Count xi in;
Found = Backtracking( i+1 );
if ( !Found )Undo( i );
/* recover to (x1, ..., xi-1) */
}
if ( Found ) break;
}
return Found;
}
考虑对称性可以少算不少
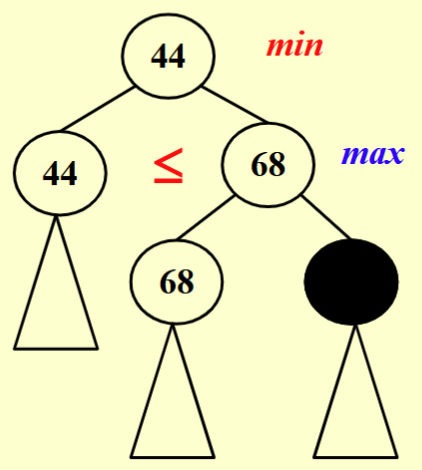
min-max搜索
以棋类游戏(三子棋为例)评估一个情况的优劣为其所有后继中估值最低的那种,从而得到最优解。围棋这类,只需模糊搜索评估的优劣比人强就行。
- 找到比另一分支更小的结果可以直接停掉
- 定义某局面的”goodness”为如下等式
其中W表示在P局面下获胜的结局数。
computer的目标是使其最大化,人类反之,因而搜索呈现一层取min一层取max的 状态。
pruning
- pruning : 在求 max 的层向下搜索(则本层是取min),如果计算出比当前解更小的解就无需再搜索
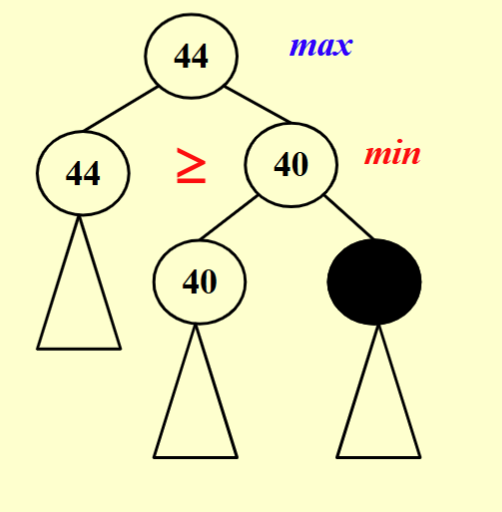
- pruning : 在求 min 的层向下搜索(则本层取max),若计算出比当前已知解更大的解就无需再搜索
Divide and Conquer
重点是主定理
主定理
一些数学推导基础
- 对 的推导
若后面那坨东西复杂度不高于 ,则总复杂度就是
一个值得关注的临界是 ,这意味着 与 等同,后面的级数和大致由 划定界限。
形式1
- 若 使得 ,则
- 若 ,则
- 若 使得 ,且存在常数 使得 则
形式2
- 若 使得 ,则
- 若 ,则
- 若 使得 ,则
形式3
的解
DP
范例:矩阵乘法次序决定
f[l][r] 为完成 l 到 r 的乘法的最小次数,则
卡特兰数
矩阵乘法的方案数
通项公式
对应实例
- 出栈次序
- 括号匹配
DP 问题的特点
- Optimal Substructure
样例:BST建立
| break | case | char | do | return | switch | void |
|---|---|---|---|---|---|---|
| 0.22 | 0.18 | 0.20 | 0.05 | 0.25 | 0.02 | 0.08 |
建立BST使得 最小
记 为 i 到 j 区间二叉树建好后的代价
样例:Floyd
Greedy
- 当且仅当局部最优解和全局最优解重合时有效,否则正确性无法保证
- 但是一般乱搞离最优解不会太远
例题
给定一系列活动 ,每个活动占据时间 ,要求合理安排使得安排活动数量最大化
my idea:
离散化,枚举每个活动 ,前缀 min 可以维护,总复杂度
按结束时间第一关键字(升序)开始时间第二关键字(降序)排列,能塞就塞
证明
Consider any nonempty subproblem ,and let be an activity in with the earliest finish time. Then is included in some maximum-size subset of mutually compatible activities of .
若 是一个最优解集合
若 无需证明
否则将 中的最早结束的活动替换为 仍然合法
哈夫曼编码树
依据出现频率编码,形成的二叉树只在叶节点对应字符的编码
code
void Huffman ( PriorityQueue heap[ ], int C ){
consider the C characters as C single node binary trees,and initialize them into a min heap;
for ( i = 1; i < C; i++ ) {
create a new node;
/* be greedy here */
delete root from min heap and attach it to left_child of node;
delete root from min heap and attach it to right_child of node;
weight of node = sum of weights of its children;
/* weight of a tree = sum of the frequencies of its leaves */
insert node into min heap;
}
}
证明
待理解补全
