普物公式整理#
前面没空做了
Chapter28 电势能、电势#
- ΔUa→b=−∫abF⋅dl,若定义 U∞=0 则 Up=∫p∞F⋅dl
- 力矩 τ=p×E
- 由此定义的 U=−p⋅E
- V=q0U 若定义 V∞=0 则 Vp=∫p∞E⋅dl
从 E 到 V : Vp=∫p∞E⋅dl
从 V 到 E : E=−∇V
- 静电场环路定理 ∮E⋅dl=0∇×E=0
注:对于变化的电场,有(参见Chapter34)
∮E⋅dl=−dtdΦB∇×E=−∂t∂B点电荷
- U(r)=4πϵ0rq1q2
- V(r)=4πϵ0rq
电偶极矩
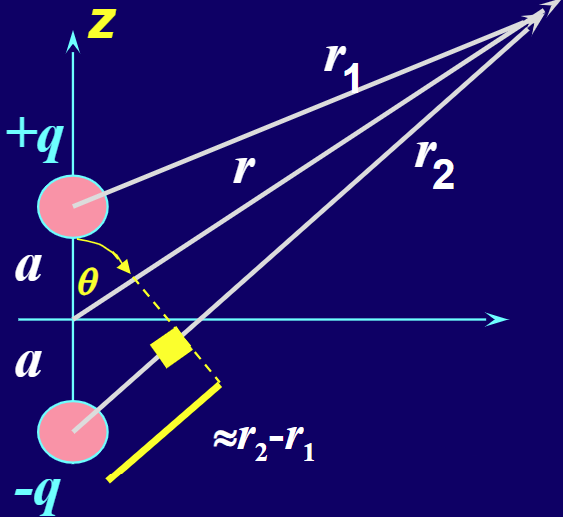
V(r)=4πϵ0q(r11−r21)≈4πϵ0r2p⋅r^如果使用 r−θ 的坐标系
V(r,θ)=4πϵ0r22aqcosθ⇒E=4πϵ0r3p((2cosθ)r^+(sinθ)θ^)- 电四偶极矩
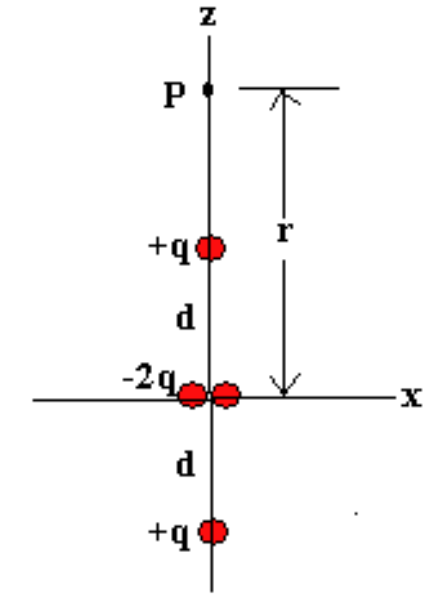
$$ \begin{aligned} V(r) &= \frac{1}{4\pi\epsilon_0}\frac{Q}{r^3(1-d^2/r^2)}\\ Q &= 2qd^2(Electric\ quadrupole\ moment) \end{aligned} $$
- 带电球壳
(Gauss′ Law⇒)E={4πϵ0r2q,r>R0,r≤R⇒V(r)={4πϵ0rq,r>R4πϵ0Rq,r≤R 电势能:微元
U&=\sum_{1\le i<j\le n} \frac{q_iq_j}{4\pi\epsilon_0r_{ij}} =\frac{1}{2}\sum_{i=1}^n\sum_{j=1}^n\frac{q_iq_j}{4\pi\epsilon_0r_{ij}}\\ &=\frac{1}{2}\sum_{i=1}^n q_iV_i =\frac{1}{2}\int Vdq =\frac{1}{2}\frac{q}{4\pi\epsilon_0R}q\\ &= \frac{q^2}{8\pi\epsilon_0R}- 带电圆环
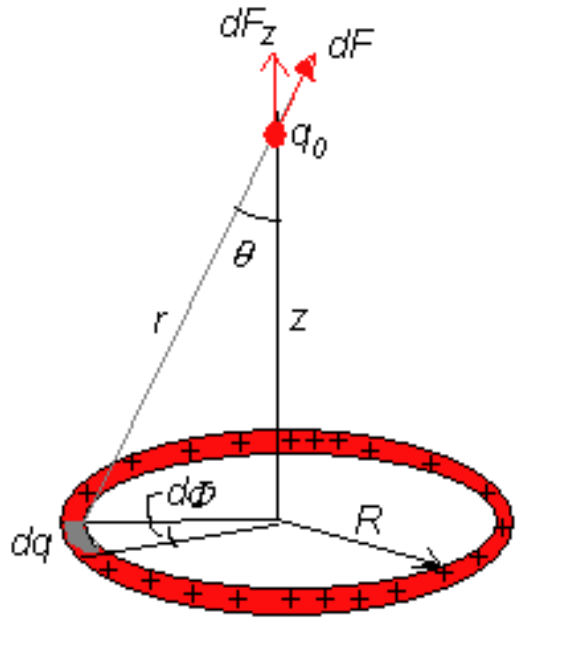
$$ V=\int dV = \frac{1}{4\pi\epsilon_0}\oint \frac{\lambda ds}{r} = \frac{q}{4\pi\epsilon_0} \frac{1}{\sqrt{z^2+R^2}} $$
- 带电圆盘
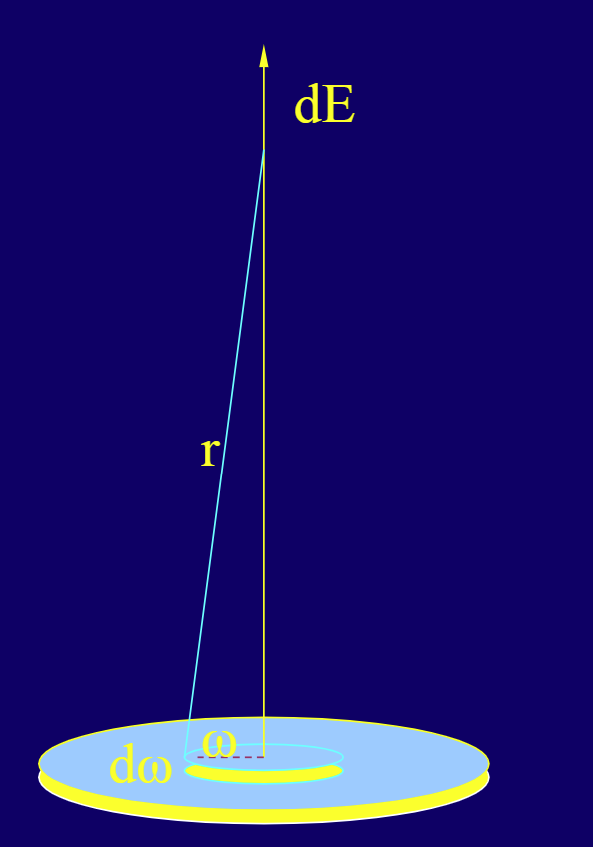
$$ \begin{aligned} V&=\int_0^R \frac{dq}{4\pi\epsilon_0} \frac{1}{\sqrt{z^2+w^2}} \\ &=\int_0^R \frac{2\pi wdw\sigma}{4\pi\epsilon_0} \frac{1}{\sqrt{z^2+w^2}}\\ &=\frac{\sigma}{2\epsilon_0}(\sqrt{z^2+R^2}-z)\\ \\ &if(z>>R)\ V = \frac{q}{4\pi\epsilon_0z}\\ \\ \\ E &= -\nabla V = -\frac{\partial V}{\partial z} = - \frac{\sigma}{2\epsilon_0}(1-\frac{1}{\sqrt{1+R^2/z^2}}) \end{aligned} $$
尖端放电
在电势相同的情况下,尖端附近电场更强,容易放电
镜像法处理感应电荷分布
感应电荷可以等效成一个导体内的镜像电荷,从而达到在导体表面产生电场与源电荷电场相抵消的效果
Chapter29(30) 电容(capacitance)和电介质(dielectrics)#
电容 C=ΔVq
电容的串并联
- 串联: C=C1+C2
- 并联: C1=C11+C21
电场能量密度(单位体积电场中的能量) uE=21ϵ0E2
推导(以平行板为例):
给电容器充电 U=C1∫0Qqdq=21CQ2 同时也 U=21CV2
U=21Aϵ0/dQ2 且 E=ϵ0σ=ϵ0AQ ⇒U=21E2ϵ0Ad
uE=volumeW=AdU=21ϵ0E2
例题:验证该 uE 适用于圆筒形电容器(tip: 即将用 U=∫uEdv 得到的结果与预期进行比较)
介电常数 κe : C=κeC0 介电常数表现了电容器中使用该种介质与真空相比的电容差距(总是大于1)
微观理解
- 对于无极分子电介质,初始 p=qd=0 ,在 E0 作用下 p=0 从而在两端产生正负电荷。产生束缚电荷,反向的电场。“电子位移极化”
- 对于有极分子电介质,初始 p 方向混乱,求和为 0,在 E0 作用下方向统一从而在两端产生正负电荷。“取向极化”(当然也存在电子位移极化,然而相比之下效应太小,仅在电场高频变化的时候比较明显)
极化强度矢量 P=ΔV∑pi
- 介质表面的σ : σ=P⋅n(n是法向量)
- 计算思路 P⇒σe′⇒E′⇒E (E′是在理解过程中认定介质产生的束缚电荷的电场,名为退极化场depolarization field,E 是最后表现出来的电场)
- 可用的一个式子 ∬P⋅dA=−∑qin
极化率 χe : 对于一般的具有各向同性的材料,有 P=χeϵ0E
- κe=1+χe
电位移矢量(电感应强度)D=ϵ0E+P
- 介质中的高斯定律
∬D⋅dA=∑qin note:此处的 qin 指的是内部的自由电荷(也即束缚电荷不算在内)
- 环路定律不成立 ∮D⋅dl=0 因为 κe 在不同路径不一样
平行板电容器
C=ΔVq=κeϵ0σdσA=κedϵ0A圆筒形电容器
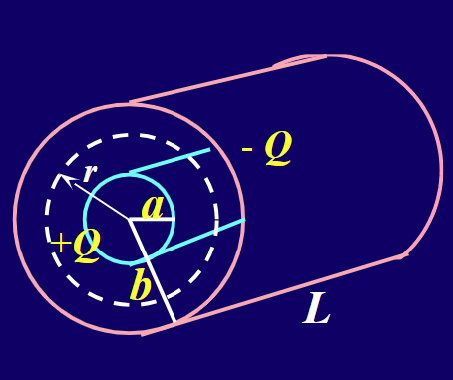
$$ C=\frac{q}{\Delta V} = \frac{\kappa_eQ}{\int_a^b \frac{Q}{2\pi\epsilon_0rL}dr}=\kappa_e\dfrac{2\pi\epsilon_0L}{\ln{\frac{b}{a}}} $$
- 球形电容器
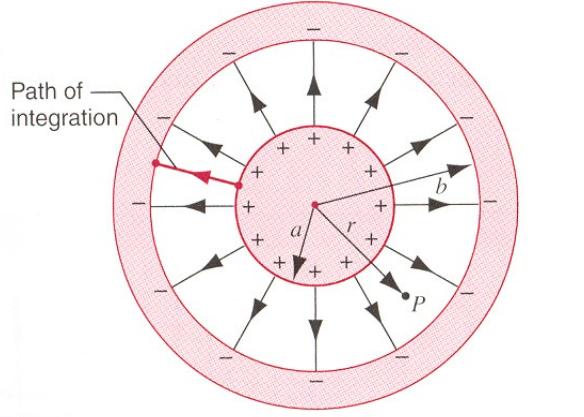
$$ C=\frac{q}{\Delta V} = \kappa_e\frac{q}{\int_a^b \frac{q}{4\pi\epsilon_0r^2}dr}=\kappa_e\dfrac{4\pi\epsilon_0ab}{b-a} $$ 令 $b\rightarrow \infin$ ,单独一个球也是电容器, $C=4\kappa_e\pi\epsilon_0a$
- 球体介质在电场中的退极化场
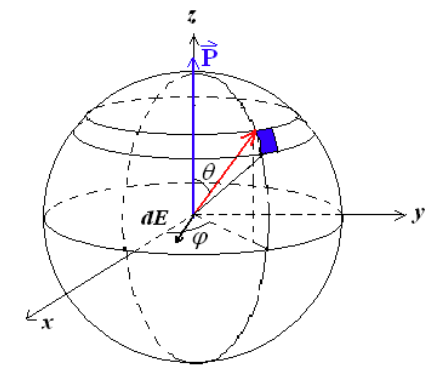
取表面的微元(蓝色部分)
σe′dE′dAdEz′Ez′=Pcosθ=4πϵ0R2dq′=4πϵ0R2σe′dA=4πϵ0R2PcosθdA=RdθRsinθdφ=−dE′cosθ=4πϵ0Pcosθsinθdθdφ=∬dEz′=−3ϵ0PChapter31 恒定电流#
- 电流强度 i=dtdq
- 电流密度矢量 j di=j⋅dA
- ∬Aj⋅dA=−dtdq
- 恒定电流的电流场有 ∬Aj⋅dA=0
- 电阻率和电导率
- R=ρAL
- ρ 电阻率, σ=ρ1 电导率
- 对于金属在一定范围内有 ρ(T)=ρ0+αT
- 电功率 P=ΔtW
- 电动势 ϵ=∫−+K⋅dl
- 把单位正电荷从负极由电源内部移到正极的非静电力做功
欧姆定律 R=dIdV
- 微分形式: j=σE
Δij=RΔV⇒jΔA=ρΔAΔlEΔl=ρE=σE
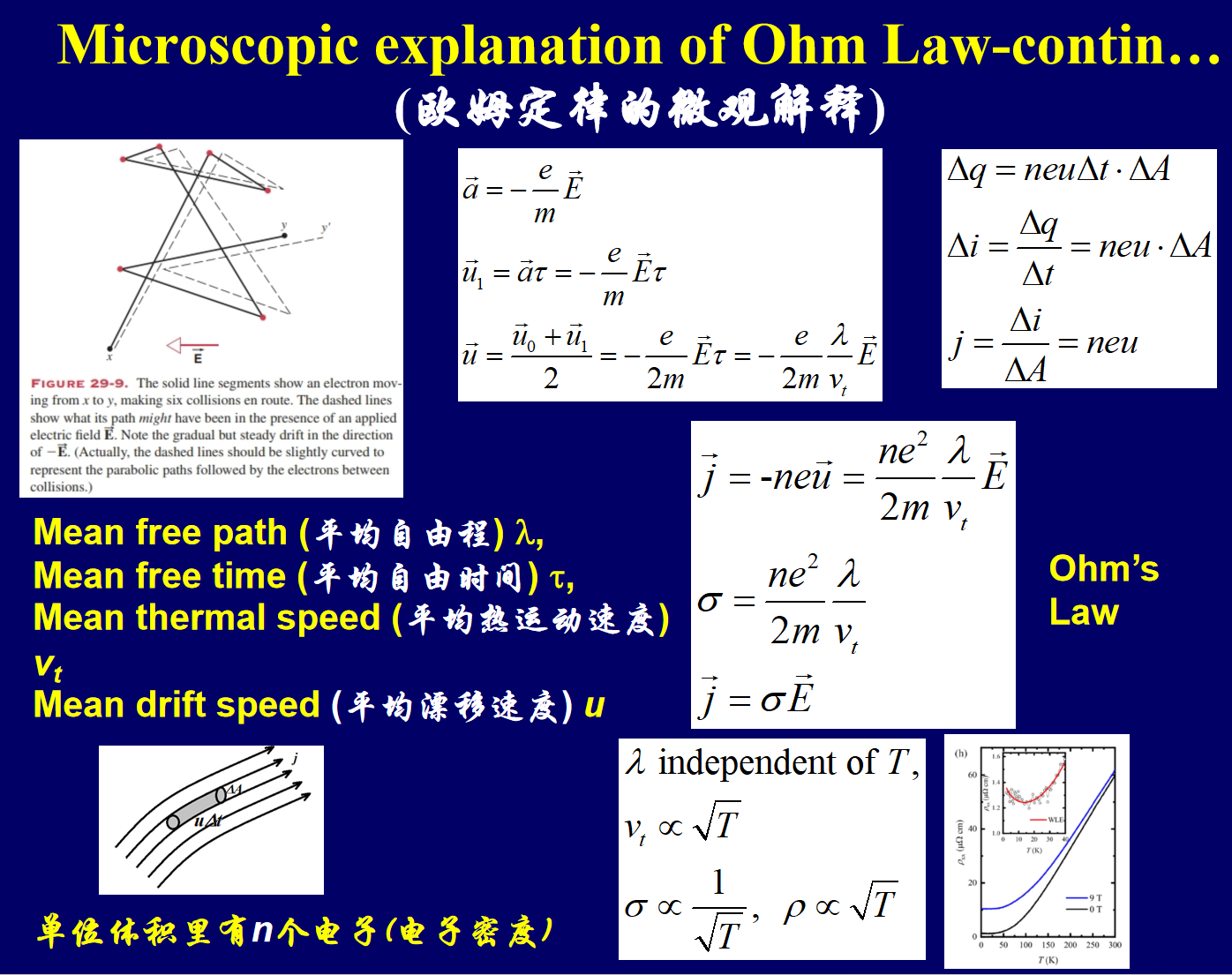
- 焦耳定律 P=i2R=RV2
- 电极的接地电阻
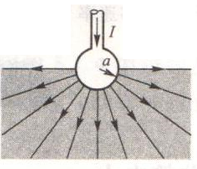
视为多层球壳作电阻
R=∫ρAdl=∫a∞ρ2πr2dr=2πaρChapter 32(33) 稳恒磁场#
- 磁感应强度 B=4πμ0∮r122i1ds1×r12^
- 单位 1T=1N/(m⋅A)
- 磁力 dF=i2ds2×B
- 磁偶极矩 μm=iAn
- 如果多匝线圈要乘以相应的线圈匝数
- 方向为 A 的法向方向(n)
- 力矩 τ=iA(n×B)=μm×B
- 由此定义的 U=−μm⋅B(貌似都是 - X偶极矩 点乘 X场)
- 洛伦兹力 f=qv×B
- F=ids×B对应的微观描述
Biot-Savart Law
其实就是 B=4πμ0∮r122i1ds1×r12^
高斯定律
∬B⋅dA=0∇⋅B=0磁场安培环路定律
∮B⋅dl=μ0in loop∑inotes
- i 的符号: 符合右手定则为正,反之为负
- 如果多次穿入穿出则要多次计算
长直导线
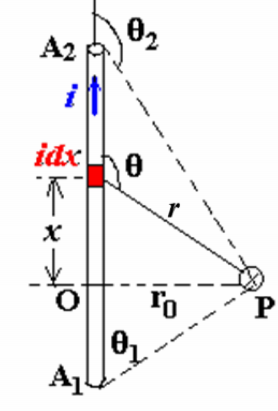 $$ B=\frac{\mu_0 i}{4\pi r_0}(\cos{\theta_1} -\cos{\theta_2}) $$ 无穷长导线则有(可用安培环路) $$ B=\frac{\mu_0 i}{2\pi r_0} $$
$$ B=\frac{\mu_0 i}{4\pi r_0}(\cos{\theta_1} -\cos{\theta_2}) $$ 无穷长导线则有(可用安培环路) $$ B=\frac{\mu_0 i}{2\pi r_0} $$
补充:导线内部:
B=2πR2μ0ir- 环形导线
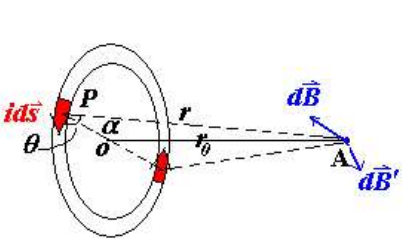
$$ B =\frac{\mu_0}{2}\frac{iR^2}{(R^2+r_0^2)^{3/2}} = \frac{\mu_0}{2\pi}\frac{\mu}{(R^2+r_0^2)^{3/2}} $$ 若在导线正中则有 $$ B=\frac{\mu_0 i}{2R} $$ 若距离很远则有 $$ B=\frac{\mu_0 iR^2}{2r_0^3} $$
- 大平板
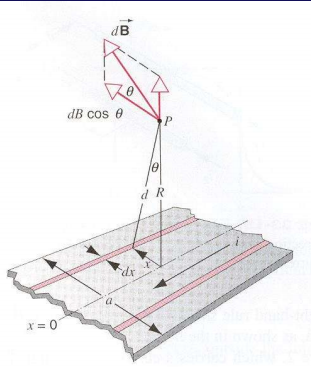
$$ B_x=\frac{\mu_0 i}{\pi a} \arctan{\frac{a}{2R}} $$ 若离平板很近则有 $$ B=\frac{\mu_0 i}{2\pi R} $$ 若离平板很远则有 $$ B=\frac{\mu_0 i}{2a} $$
- 螺旋管
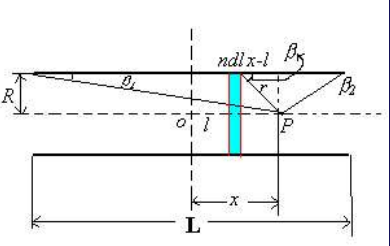
$$ B=\frac{1}{2}\mu_0ni(\cos{\beta_1}-\cos{\beta_2}) $$ 如果螺线管无限长 $$ B=\mu_0ni $$ 这个也可以用安培环路计算

如果在螺线管一端
B=21μ0ni- 多层螺线管
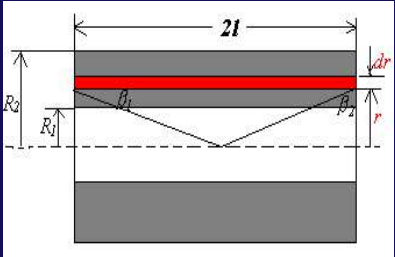
- 各层加起来的总匝数:N
- ni=LNi⇒jdr=2l(R2−R1)Nidr
B=μ0jllnR2+R22+l2R2+R22+l2- 无限大电流板
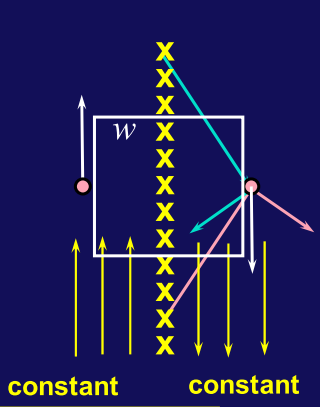
$$ \oint \vec{V}\cdot\vec{dl} = 2Bw = \mu_0nwi\\ B=\frac{1}{2}\mu_0ni $$
螺绕环(Toroid)
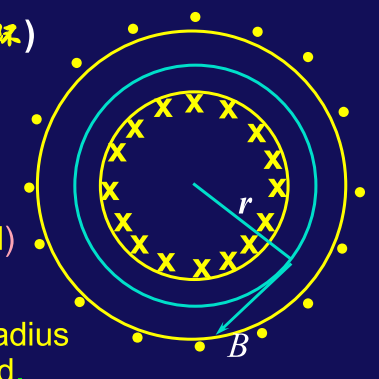
∮B⋅dl=μ0NiB=μ0ni
质谱仪
瓷瓶
动量仪
回旋加速器
加速到一定程度后相对论效应明显,需要特别设置磁场
霍尔效应
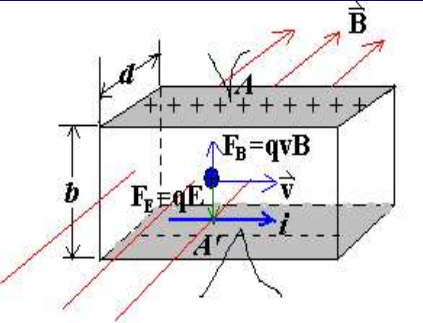
VAA′=nq1diB=κdiB- Hall Resistance RH=iVAA′=nqdB
- 载流子密度 n=qdiBVAA′1
Chapter 34&35(36) 法拉第电磁感应定律 & 电感(Inductance) 和材料磁性性质#
磁通量 ΦB=∬B⋅dA
磁通匝链数 Ψ=NΦB
动生电动势 ϵ=∫−+(v×B)⋅dl
- 绕一端旋转的棒 ϵ=−21BωR2
互感系数 M=iΨ
- 单位 : 1H=1Wb/1A
- 互感系数和两线圈自感系数的关系:
No flux leakage:M=L1L2Direct in series:L=L1+L2+2MOpposite in series:L=L1+L2−2M自感系数:线圈自己由于电流变化产生感应电动势对自己的影响的衡量 L=iΨ
- ϵL=−dtdΨ=−Ldtdi
磁导率permeability constant κm
- 线圈插入磁性材料,L=κmL0
- 顺磁逆磁 κm≈1 ,铁磁材料 κm≈103−104
磁化强度矢量 M=ΔV∑μm
磁场强度 H=μ0B−M
磁化率susceptibility magnetization coefficient χm
- κm=1+χm
- 法拉第电磁感应定律
ϵ=−dtdΦB ⇒{∮E⋅dl=−dtdΦB∇×E=−∂t∂B- 楞次定律
The induced current will appear in such a direction that it opposes the change in flux that produced it.
- 磁性材料加入后的安培环路定律和高斯定律
∮lH⋅dl=inl∑i0∬B⋅dA=0- 螺线圈的自感系数

L=iΨ=inlμ0niA=μ0n2lALv=lAL=μ0n2- 长方形螺绕环的自感系数
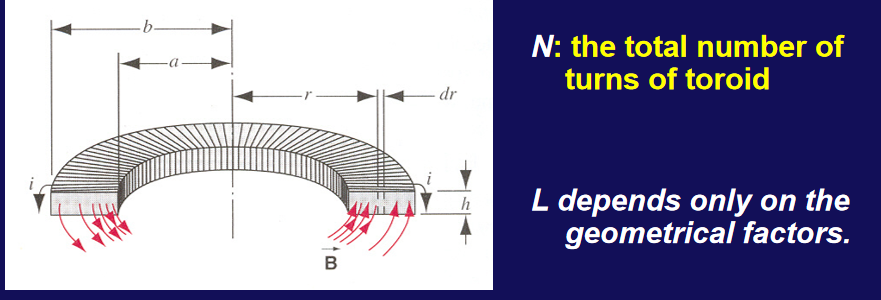
∮B⋅dl=μ0Ni⇒B=2πrμ0iNΦB=∬B⋅dA=2πμ0iNhlnabL=2πμ0iN2hlnab- 同轴电缆
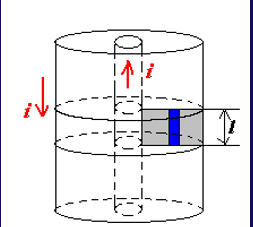
B=2πrμ0iΦB=∫R1R2Bldr=2πrμ0illnR1R2- RC电路与RL电路
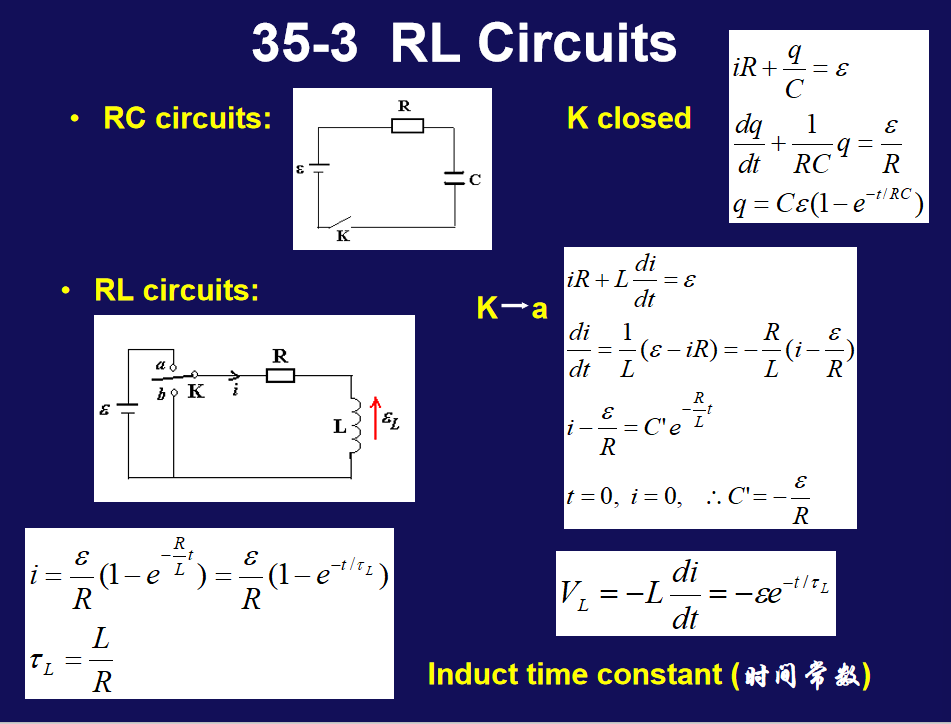
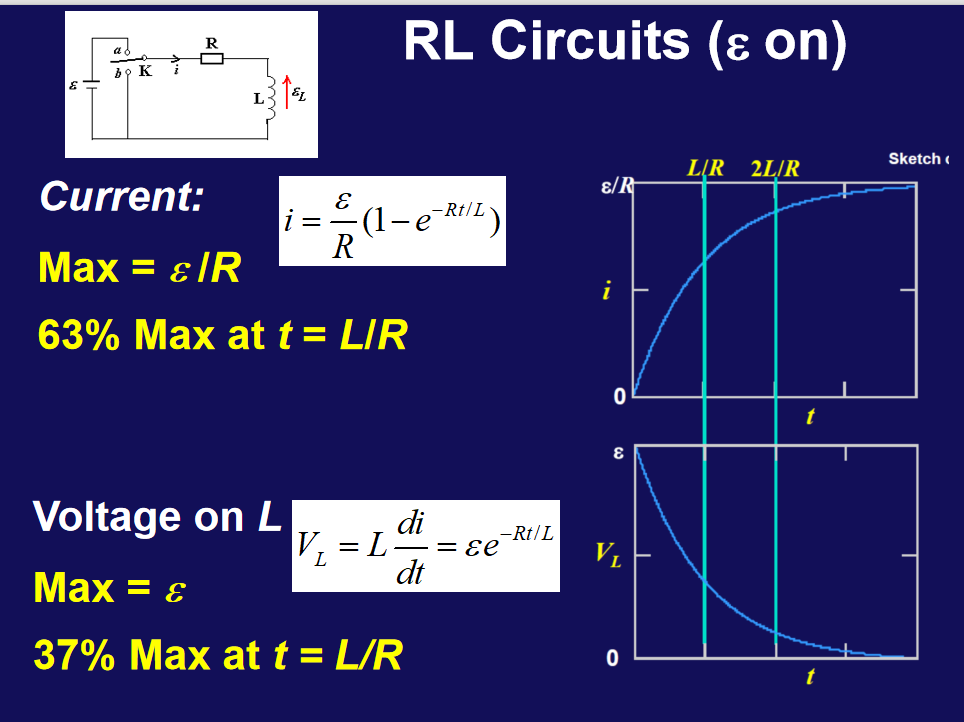

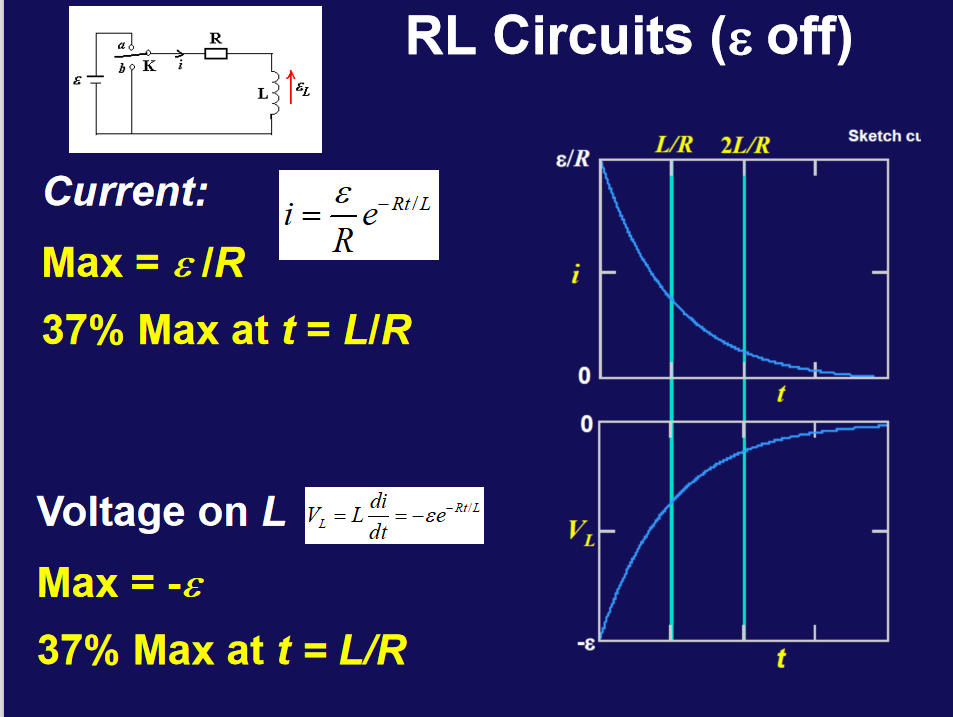
- LC振荡电路
| 简谐运动 | 电磁震荡 |
|---|
| 弹簧 Us=21kx2 | 电容 UE=21Cq2 |
| 木块 K=21mv2 | 电感 UB=21Li2 |
| v=dtdx | i=dtdq |
| ω=mk | ω=LC1 |
dtdU=d(21Li2+21Cq2)=Lidtdi+Cqdtdq=Lidt2d2q+Cqi=0⇒dt2d2q+LC1q=0⇒q=qmcos(ωt+φ),ω=LC1t=0,q=qm,φ=0- RLC电路
Ldtdi+iR+Cq={ϵ,K→a0,K→b当λ2=4acb2=4LC1R2>1 时
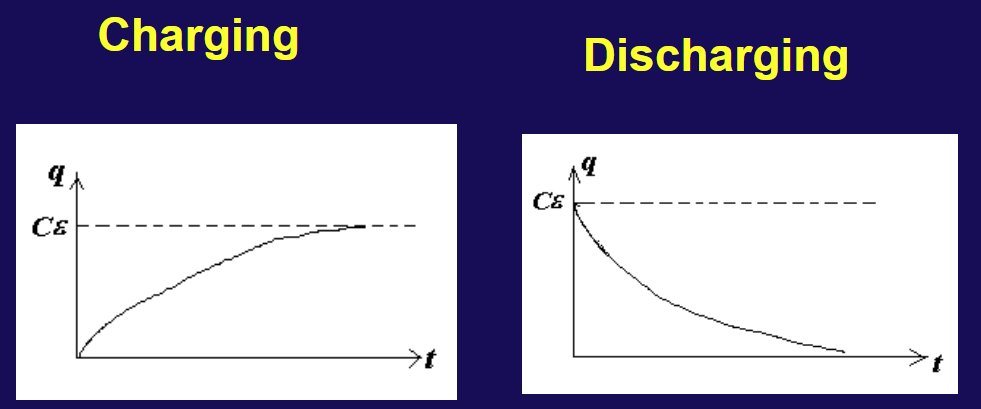
当 λ=2RLC=1 时
- q=e−2LRt(A+Bt)+Cϵ
- 称为临界阻尼,图像如下
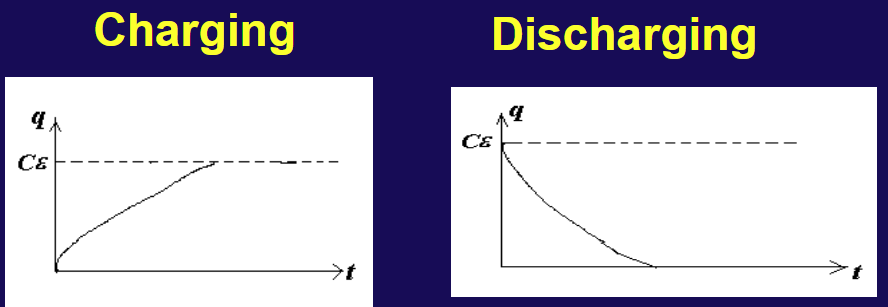
当 λ=2RLC
- q=qme−2LRtcos(ωt+φ)+Cϵ
- ω=ω02−(2LR)2
- 称为阻尼振荡,图像如下
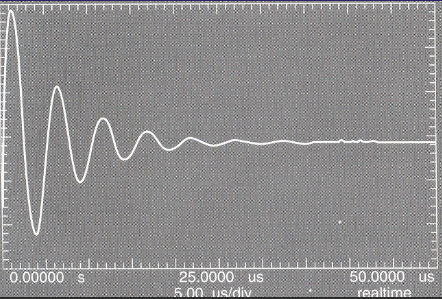
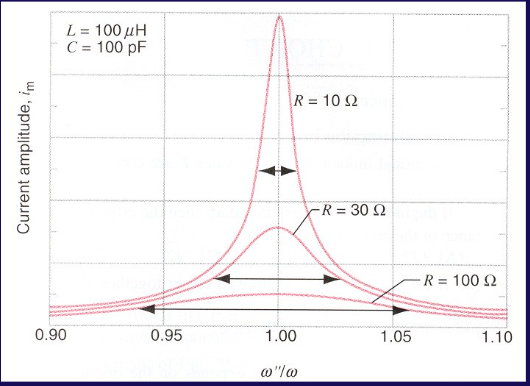
- 若 ϵ=ϵmcosω′′t,则随着 ω′′ 变化振幅变化如下
- 涡流
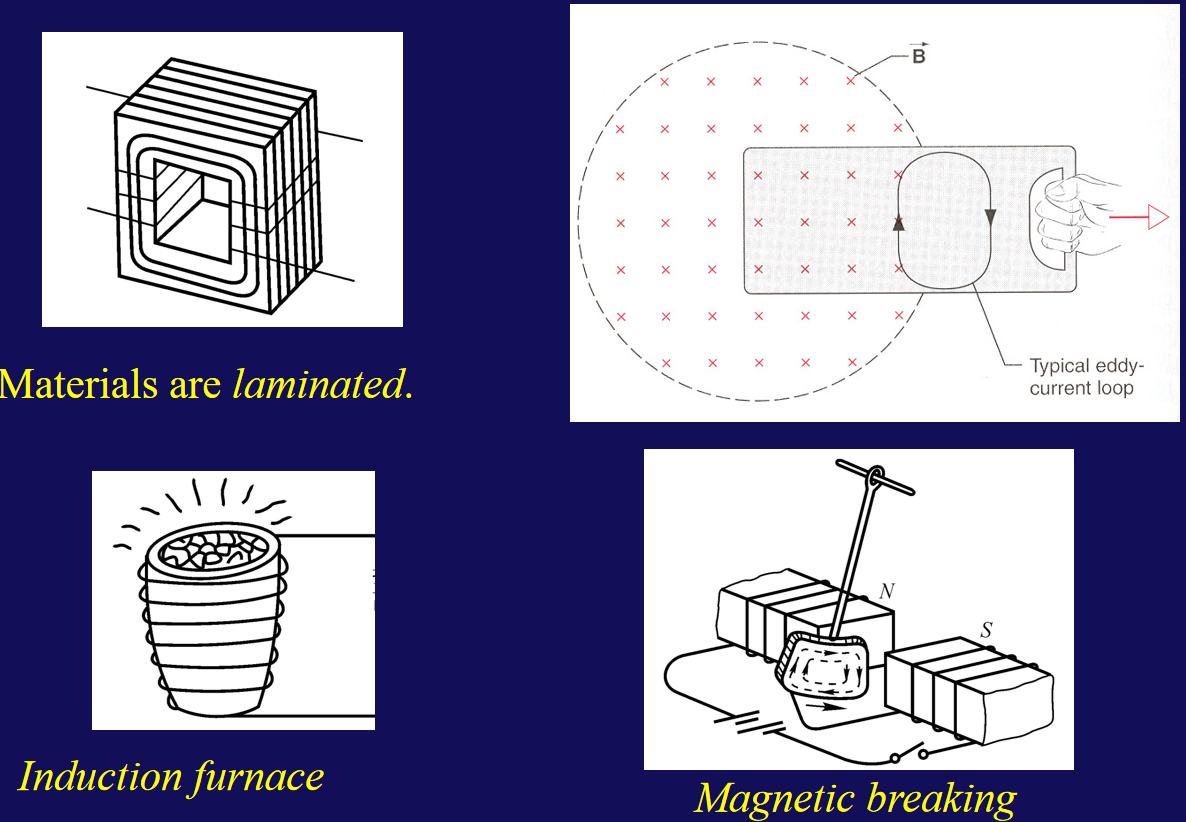
- 电磁炮
弹丸中感生电动势导致涡流,与线圈的磁场相互作用导致发射
- 磁悬浮
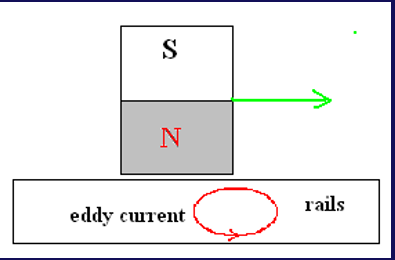
- 发电机
ΦB=BAcosωtϵ=BAωsinωt 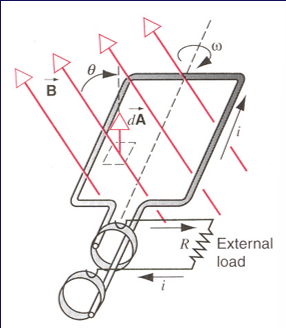
- 电子加速器
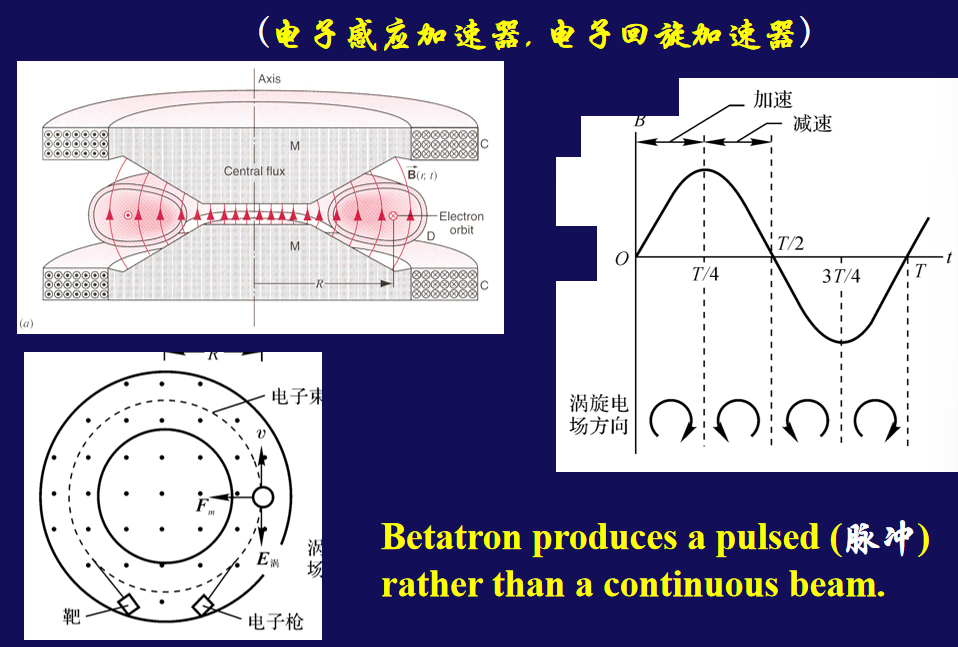
- B 和 v都在变化,最终呈现效果是 R 没变
- 因为会反向增加所以产出不持续

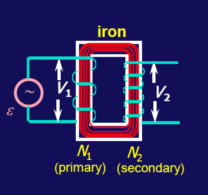
- 变压器
利用 M12=M21 得到 V2=N1N2V1
一些杂七杂八我并看不懂的东西#
- 轨道磁矩 μl=−2meL
- 其中 L=L(L+1)2πh
- ℏ=2πh
- 自旋磁矩
- 费米子 s=22k+1ℏ
- 玻色子 s=kℏ
- 铁磁材料的磁滞回线
- 铁磁材料内存在若干分块(磁畴),分块内部磁偶极矩方向相同
- 施加磁场能让磁偶极矩方向相同,即使退磁后也不能完全恢复到随机化,因而 B=0 (称为剩磁)
总结对比:电与磁#
| 电 | 磁 |
|---|
| 非常重要的常数 | ϵ0≈8.86×10−12F/m | μ0=4π×10−7H/m |
| 初始安培环路定理 | ∬E⋅dA=∑qin | ∮lB⋅dl=∑inli0 |
| 初始高斯定律 | ∮lE⋅dl=0 | ∬B⋅dA=0 |
| 由于介质引入的新物理量 | 电感应强度 D=ϵ0E+P | 磁场强度 H=μ0B−M |
| 电容 C=VQ | 电感 L=iΨ |
| 引入介质的安培环路定律 | \ | ∮lH⋅dl=∑inli0 |
| 引入介质的高斯定律 | ∬D⋅dA=∑qin | \ |
| χ | 极化率 χe | 磁化率 χm |
| χ 的引入 | 对于一般的具有各向同性的材料,有 P=χeϵ0E | 对于磁性材料 M=χmH |
| κ 的引入 | 插入介质后 C=κeC0 | 插入磁性材料后 L=κmL0
B=χmμ0H |
| κ | 节点常数 κe=1+χe | 磁导率 κm=1+χm |
| X化强度矢量 | 极化强度矢量 P=ΔV∑pi | 磁化强度矢量M=ΔV∑μm |
| X场能量密度 | 电场能量密度uE=21ϵ0E2=21D⋅E | 磁场能量密度 uB=21μ0B2=21B⋅H |
Chapter 38 麦克斯韦方程组#
公式推导#
新的安培环路定律
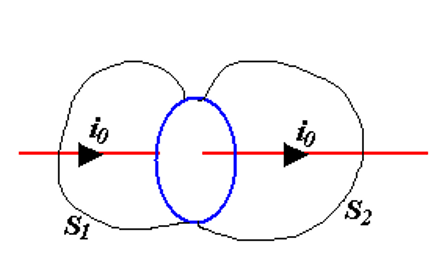
∮H⋅dl=∬S2j0⋅dA=−∬S1j0⋅dA=i0⇒∬Sj0⋅dA=∬S2j0⋅dA+∬S1j0⋅dA=0同时根据stolz公式我们又有
∮H⋅dl=∬S2(∇×H)⋅dA但是存在问题:在电容的情况下不成立(如图中闭合曲面3)
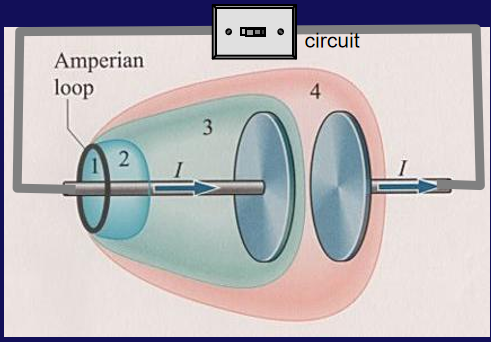
⇒ 变化的电场应当算入其中!
引入变量:
电位移通量 ΦD=∬D⋅dA, 位移电流 iD=dtdΦD=∬
∮H⋅dl=i0+iD=∬(j0+∂t∂D)⋅dA
Chapter39#
中间漏了好多,有空补上
电磁波的能流密度(Energy Flux Density)与动量#
dtdU=dtd∭(21D⋅E+21B⋅H)=21∭∂t∂(D⋅E+B⋅H)dv ∂t∂(D⋅E+B⋅H)=κeϵ0∂t∂(E⋅E)+κmμ0∂t∂(H⋅H)=2κeϵ0E⋅∂t∂E+2κmμ0H⋅∂t∂H=2E⋅∂t∂D+2H⋅∂t∂B由麦克斯韦方程组
∂t∂D=∂t∂B=
 $$ \begin{aligned} V(r) &= \frac{1}{4\pi\epsilon_0}\frac{Q}{r^3(1-d^2/r^2)}\\ Q &= 2qd^2(Electric\ quadrupole\ moment) \end{aligned} $$
$$ \begin{aligned} V(r) &= \frac{1}{4\pi\epsilon_0}\frac{Q}{r^3(1-d^2/r^2)}\\ Q &= 2qd^2(Electric\ quadrupole\ moment) \end{aligned} $$ $$ V=\int dV = \frac{1}{4\pi\epsilon_0}\oint \frac{\lambda ds}{r} = \frac{q}{4\pi\epsilon_0} \frac{1}{\sqrt{z^2+R^2}} $$
$$ V=\int dV = \frac{1}{4\pi\epsilon_0}\oint \frac{\lambda ds}{r} = \frac{q}{4\pi\epsilon_0} \frac{1}{\sqrt{z^2+R^2}} $$ $$ \begin{aligned} V&=\int_0^R \frac{dq}{4\pi\epsilon_0} \frac{1}{\sqrt{z^2+w^2}} \\ &=\int_0^R \frac{2\pi wdw\sigma}{4\pi\epsilon_0} \frac{1}{\sqrt{z^2+w^2}}\\ &=\frac{\sigma}{2\epsilon_0}(\sqrt{z^2+R^2}-z)\\ \\ &if(z>>R)\ V = \frac{q}{4\pi\epsilon_0z}\\ \\ \\ E &= -\nabla V = -\frac{\partial V}{\partial z} = - \frac{\sigma}{2\epsilon_0}(1-\frac{1}{\sqrt{1+R^2/z^2}}) \end{aligned} $$
$$ \begin{aligned} V&=\int_0^R \frac{dq}{4\pi\epsilon_0} \frac{1}{\sqrt{z^2+w^2}} \\ &=\int_0^R \frac{2\pi wdw\sigma}{4\pi\epsilon_0} \frac{1}{\sqrt{z^2+w^2}}\\ &=\frac{\sigma}{2\epsilon_0}(\sqrt{z^2+R^2}-z)\\ \\ &if(z>>R)\ V = \frac{q}{4\pi\epsilon_0z}\\ \\ \\ E &= -\nabla V = -\frac{\partial V}{\partial z} = - \frac{\sigma}{2\epsilon_0}(1-\frac{1}{\sqrt{1+R^2/z^2}}) \end{aligned} $$ $$ C=\frac{q}{\Delta V} = \frac{\kappa_eQ}{\int_a^b \frac{Q}{2\pi\epsilon_0rL}dr}=\kappa_e\dfrac{2\pi\epsilon_0L}{\ln{\frac{b}{a}}} $$
$$ C=\frac{q}{\Delta V} = \frac{\kappa_eQ}{\int_a^b \frac{Q}{2\pi\epsilon_0rL}dr}=\kappa_e\dfrac{2\pi\epsilon_0L}{\ln{\frac{b}{a}}} $$ $$ C=\frac{q}{\Delta V} = \kappa_e\frac{q}{\int_a^b \frac{q}{4\pi\epsilon_0r^2}dr}=\kappa_e\dfrac{4\pi\epsilon_0ab}{b-a} $$ 令 $b\rightarrow \infin$ ,单独一个球也是电容器, $C=4\kappa_e\pi\epsilon_0a$
$$ C=\frac{q}{\Delta V} = \kappa_e\frac{q}{\int_a^b \frac{q}{4\pi\epsilon_0r^2}dr}=\kappa_e\dfrac{4\pi\epsilon_0ab}{b-a} $$ 令 $b\rightarrow \infin$ ,单独一个球也是电容器, $C=4\kappa_e\pi\epsilon_0a$


 $$ B=\frac{\mu_0 i}{4\pi r_0}(\cos{\theta_1} -\cos{\theta_2}) $$ 无穷长导线则有(可用安培环路) $$ B=\frac{\mu_0 i}{2\pi r_0} $$
$$ B=\frac{\mu_0 i}{4\pi r_0}(\cos{\theta_1} -\cos{\theta_2}) $$ 无穷长导线则有(可用安培环路) $$ B=\frac{\mu_0 i}{2\pi r_0} $$ $$ B =\frac{\mu_0}{2}\frac{iR^2}{(R^2+r_0^2)^{3/2}} = \frac{\mu_0}{2\pi}\frac{\mu}{(R^2+r_0^2)^{3/2}} $$ 若在导线正中则有 $$ B=\frac{\mu_0 i}{2R} $$ 若距离很远则有 $$ B=\frac{\mu_0 iR^2}{2r_0^3} $$
$$ B =\frac{\mu_0}{2}\frac{iR^2}{(R^2+r_0^2)^{3/2}} = \frac{\mu_0}{2\pi}\frac{\mu}{(R^2+r_0^2)^{3/2}} $$ 若在导线正中则有 $$ B=\frac{\mu_0 i}{2R} $$ 若距离很远则有 $$ B=\frac{\mu_0 iR^2}{2r_0^3} $$ $$ B_x=\frac{\mu_0 i}{\pi a} \arctan{\frac{a}{2R}} $$ 若离平板很近则有 $$ B=\frac{\mu_0 i}{2\pi R} $$ 若离平板很远则有 $$ B=\frac{\mu_0 i}{2a} $$
$$ B_x=\frac{\mu_0 i}{\pi a} \arctan{\frac{a}{2R}} $$ 若离平板很近则有 $$ B=\frac{\mu_0 i}{2\pi R} $$ 若离平板很远则有 $$ B=\frac{\mu_0 i}{2a} $$ $$ B=\frac{1}{2}\mu_0ni(\cos{\beta_1}-\cos{\beta_2}) $$ 如果螺线管无限长 $$ B=\mu_0ni $$ 这个也可以用安培环路计算
$$ B=\frac{1}{2}\mu_0ni(\cos{\beta_1}-\cos{\beta_2}) $$ 如果螺线管无限长 $$ B=\mu_0ni $$ 这个也可以用安培环路计算

 $$ \oint \vec{V}\cdot\vec{dl} = 2Bw = \mu_0nwi\\ B=\frac{1}{2}\mu_0ni $$
$$ \oint \vec{V}\cdot\vec{dl} = 2Bw = \mu_0nwi\\ B=\frac{1}{2}\mu_0ni $$





















