Chapter 3⚓︎
默认64bit为double word,一个word为32bit
- 补码可以直接加减,不可直接相乘!
-
(?)如(1001)2平方不会得到49,但是如果补全成(11111001)2的平方可以
-
浮点数:Single precicion ~ Quadruple precision
ALU⚓︎
- 加减法溢出条件
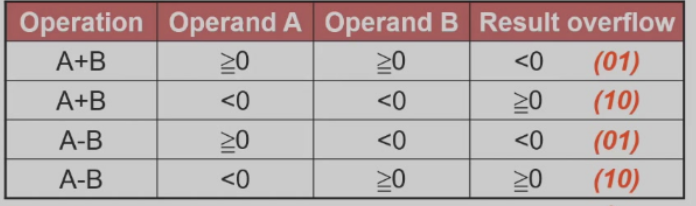
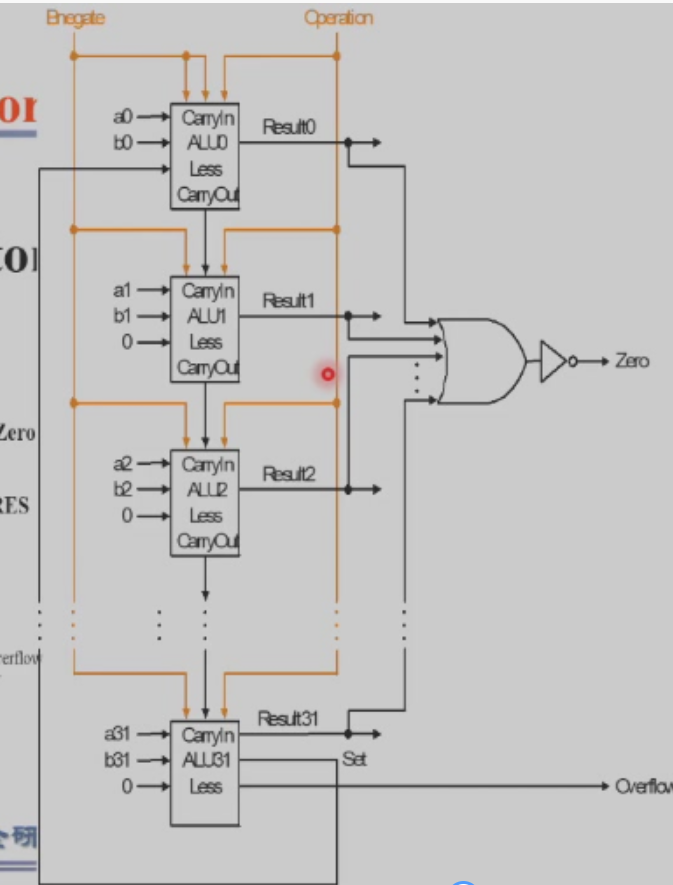
注:上图的set传到less是为了执行slt操作
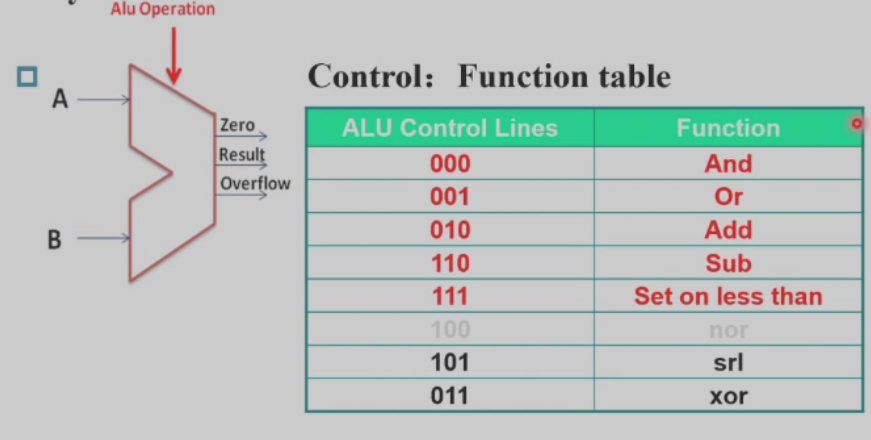
超前进位加法器⚓︎
一位版本⚓︎
\(G_i = A_i \& B_i\)(generate)
\(P_i = A_i|B_i\) (propogation)
则\(S_i = P_i \bigoplus C_i\), \(C_{i+1}=G_i+P_iC_i\)
四位版本⚓︎
对每个 \(C_i\) 进行展开,得到结果如下
\[
\begin{aligned}
C_1 &= G_0 + P_0C_0\\
C_2 &= G_1 + P_1C_1 = G_1 + P_1G_0 + P_1P_0C_0\\
C_3 &= G_2 + P_2C_2 = G_2 + P_2G_1 + P_2P_1G_0 + P_2P_1P_0C_0\\
C_4 &= G_3 + P_3C_3 = G_3 + P_3G_2 + P_3P_2G_1 + P_3P_2P_1G_0 + P_3P_2P_1P_0C_0
\end{aligned}
\]
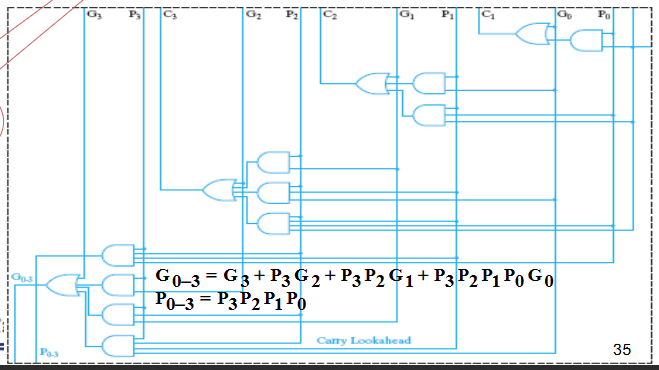
- \(C_1\) 到 \(C_4\) 同步可得
十六位版本⚓︎
- fan-in限制不能继续展开了
乘法⚓︎
-
符号问题:一般转成绝对值运算再回去
-
实操:龟速乘做法\(\rightarrow\) “山不就我我来就山” 运算结果右移,被乘数不动
\(\Rightarrow\) 乘数和结果右移同步,可以利用低位存储乘数
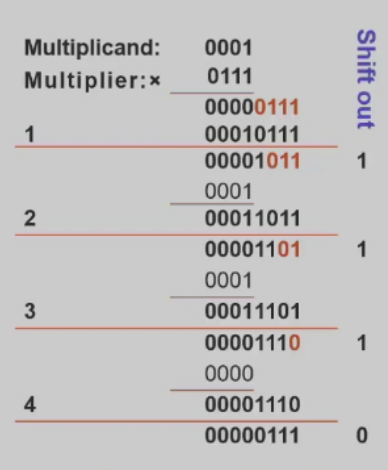
- [了解] Booth's Algorithm
Idea: 1111010-> 10000000 + 10 -1000
除法⚓︎
- 长除法的减法版本
- 允许有试减环节,不判断先减再说
- 具体操作(V1):除数存在寄存器左边,逐渐右移试减;被除数(余数)放在寄存器右边不用动
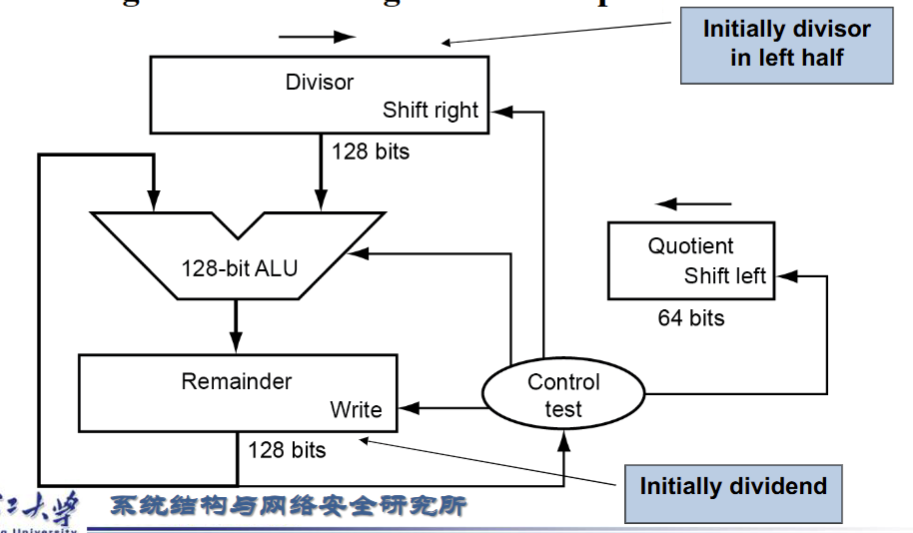
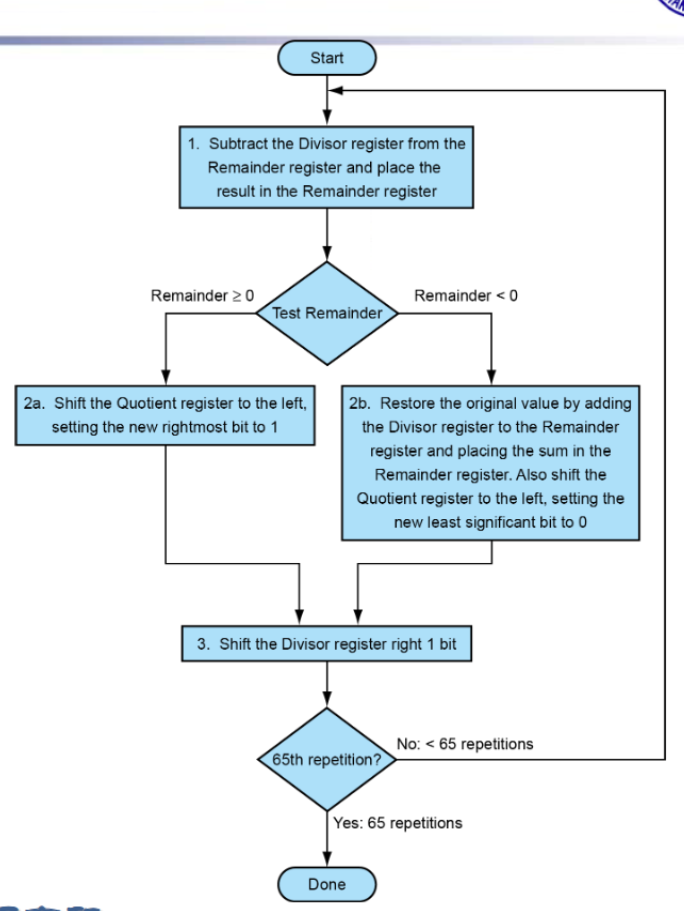
- V2(优化了存储空间):除数不用开二倍长度,Remainder寄存器将被除数放在右侧,逐步左移,Divisior对齐Remainder最左侧进行减法操作。减法结果从右侧存入Remainder充当V1的Quotient
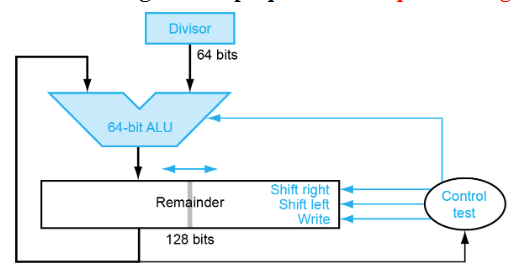
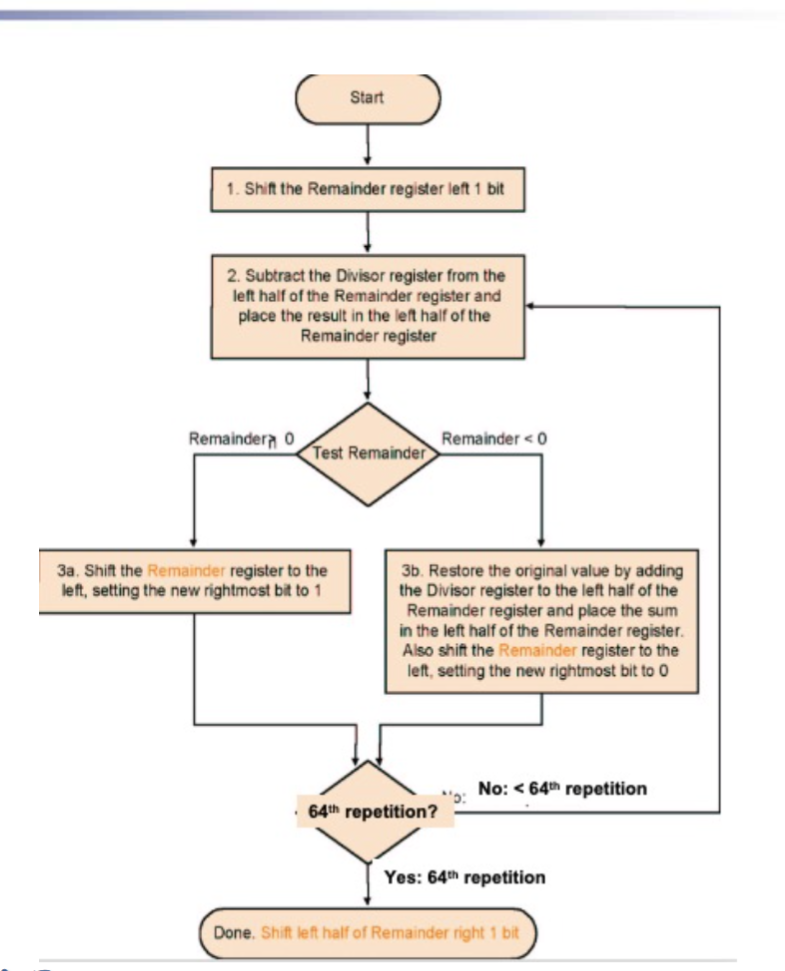
- 因为第一次减法结果必定为0,所以先左移再做减法。随之导致最后多移一次,故加上了ShiftRight接口
Q:负数除法,余数和商的符号问题?
A:Remainder和Dividend保持一致
- 除法无法并行实现:依赖前一次的结果
- [可以了解]Faster dividers(e.g. SRT division)
- Risc-V中的除法指令
- div,rem:有符号除法
- divu,remu:无符号除法
- 处理器不会对除0和溢出的情况进行报错,需要自行处理
浮点数⚓︎
仿照科学计数法,可以将浮点数记为 \((-1)^s\times F \times 2^E\) 。
- 上溢:正指数太大
- 下溢:负指数太小
表示形式⚓︎
-
RISC-V
-
float : 1位符号位+8位指数+23位尾数
-
double : 1位符号位+11位指数+52位尾数
-
IEEE 754浮点数标准:将尾数的1隐含掉(类似科学计数法没有前导零,尾数的第一位必然为1),但0是例外,其表示为 \(0....0_2\) 。例如一个浮点数尾数部分表示为 \(f_1f_2...f_n\) ,则其值实际为 \(1+0.f_1f_2f_3...f_n\) 。
-
对异常值有特殊的表示
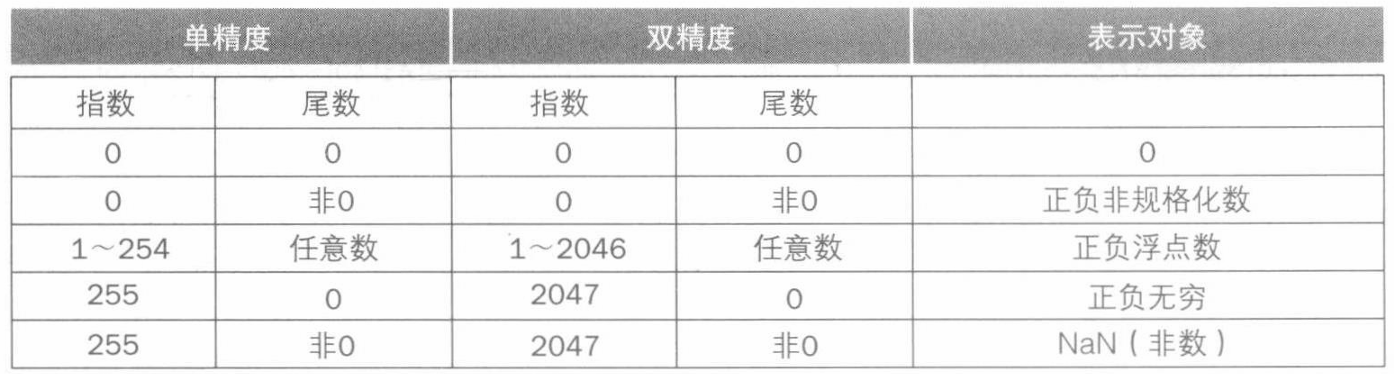
- 整个浮点数不是补码表示法而是符号-数值形式,但指数部分使用补码表示
- 移码表示法 :对指数部分加上一个偏移量以方便比较大小(类似从有符号整数到无符号整数范围的位移),IEEE 754规定 float 偏移量127, double 偏移量1023。则一个浮点数实际值为 \((-1)^S\times (1+\)有效位数\() \times 2^{exponent-bias}\) 。
- 所以float绝对值最小的是 \(\pm 1.0\times 2^{-126}\),最大的Fraction:111111,约为2.0,绝对值最大的就是\(\pm 2.0\times 2^{127}\) 。双精度分别为 \(\pm 1.0\times 2^{-1022}\) 和 \(\pm 2.0 \times 2^{1023}\)
加减⚓︎
- 对齐:指数小往指数大对齐
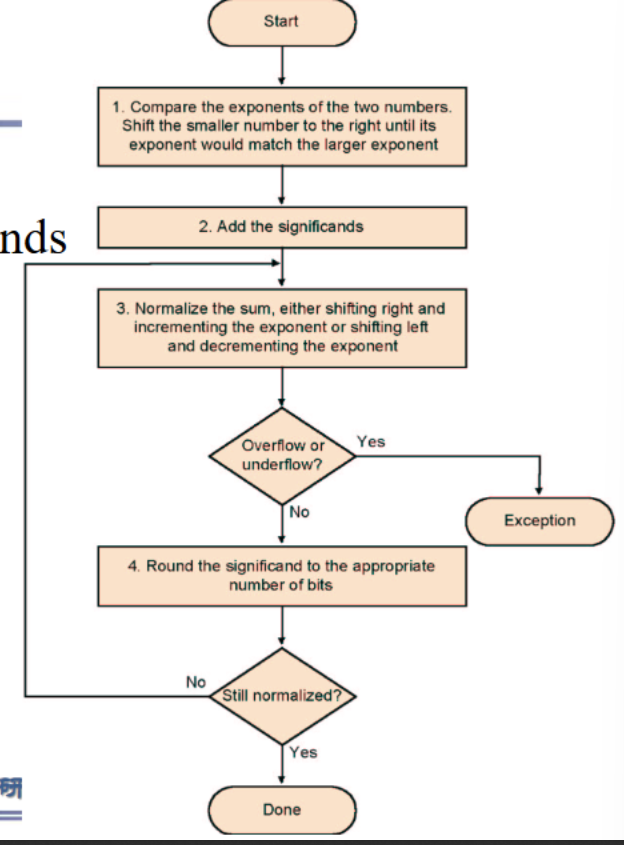
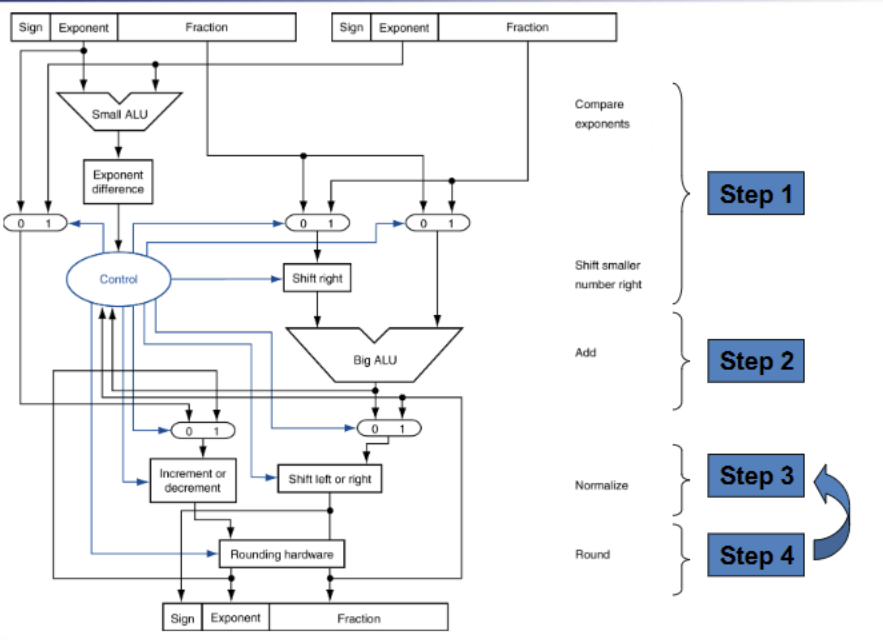
乘除⚓︎
- 指数相加(但是要把bias补回来)
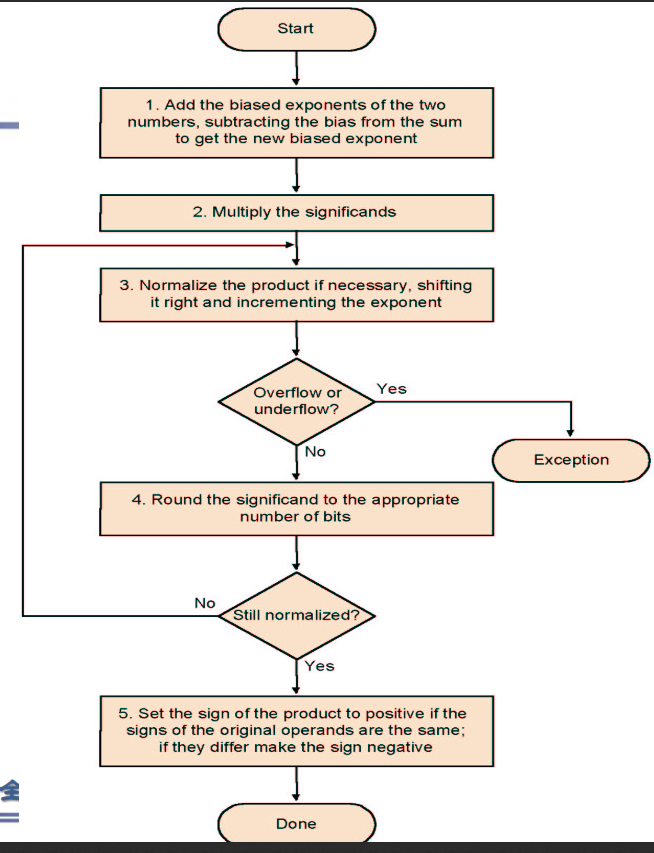
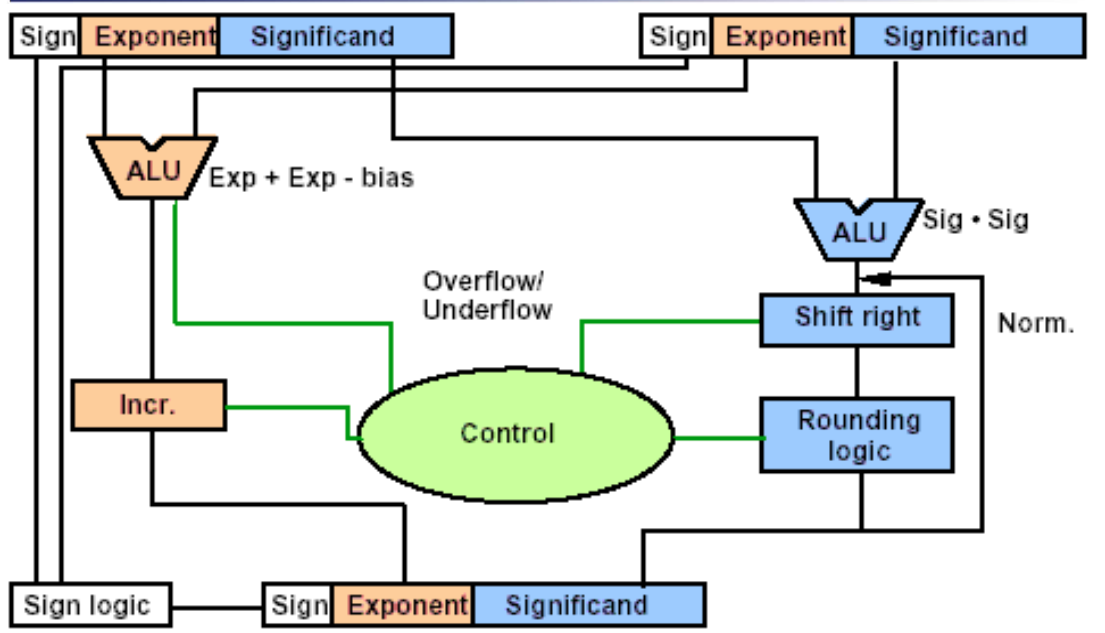
(除法类似)
Accurate Arithmetic⚓︎
- 三个extra bits(不一定系统有)
- guard:
- round:
- sticky:
- TODO:理解三个extra bits的作用并了解其在浮点数运算具体操作