跳转至

External Sorting⚓︎

这个开篇真的会梦回计组

对于内存不足以一次性排序的数据量，由于访问磁盘开销巨大（记得看看计组cache那一章），我们使用归并排序，但是希望能让磁盘访问次数尽可能最小化

  • why归并排序？ 归并能够在有限的内存中把有序数列规模增大直到有序 其他排序做得到吗.jpg

以下令内存最大容量为 \(M\) , 总数据量 \(N\) ，实行 \(k\) 路归并

一些名词
  • run : 一段数据，它应当是内部有序的
  • pass : 将 \(k\) 路数据归并到其他路的过程
  • copy : 从一路将数据分发到若干路的过程（正常不会出现在计数中，只是老师在用3 tapes做2路归并的例子时出现过）
  • tape : 一个磁盘，这里可以理解为一个无限大的存放 runs 的地方

性能优化⚓︎

Passes⚓︎

\(2k\) 个磁盘时

  • Number of passes = \(1+\lceil\log_k{N/M}\rceil\)
    • "1" 是从 \(T_1\) 向其他磁带分发 pass 的过程，由于是第一次还需要将每个 pass 内部变为有序
    • 此后每一次 pass （假设还是统一归并到 \(T_1\) ）会让 \(pass\) 数量变为 \(\frac{1}{k}\) （上取整）

老师给出的其中一个例子如下

image-20241229120325961

此时要优化passes的数量：

  1. 增加 \(k\) \(\Rightarrow\) tape数量、排序复杂度增加

  2. 算法优化：Replacement Selection

    • 可以获得更长的run从而减少passes

    在 fds 的 bonus 中应该有这个题，这是题干，可以辅助理解。

    Replacement Selection

    When the input is much too large to fit into memory, we have to do external sorting instead of internal sorting. One of the key steps in external sorting is to generate sets of sorted records (also called runs) with limited internal memory. The simplest method is to read as many records as possible into the memory, and sort them internally, then write the resulting run back to some tape. The size of each run is the same as the capacity of the internal memory.

    Replacement Selection sorting algorithm was described in 1965 by Donald Knuth. Notice that as soon as the first record is written to an output tape, the memory it used becomes available for another record. Assume that we are sorting in ascending order, if the next record is not smaller than the record we have just output, then it can be included in the run.

    For example, suppose that we have a set of input { 81, 94, 11, 96, 12, 99, 35 }, and our memory can sort 3 records only. By the simplest method we will obtain three runs: { 11, 81, 94 }, { 12, 96, 99 } and { 35 }. According to the replacement selection algorithm, we would read and sort the first 3 records { 81, 94, 11 } and output 11 as the smallest one. Then one space is available so 96 is read in and will join the first run since it is larger than 11. Now we have { 81, 94, 96 }. After 81 is out, 12 comes in but it must belong to the next run since it is smaller than 81. Hence we have { 94, 96, 12 } where 12 will stay since it belongs to the next run. When 94 is out and 99 is in, since 99 is larger than 94, it must belong to the first run. Eventually we will obtain two runs: the first one contains { 11, 81, 94, 96, 99 } and the second one contains { 12, 35 }.

Tapes:Polyphase Merge Sorting多相归并⚓︎

\(k+1\) 个磁盘

  • 合并规则有所变化：不会把现有runs的磁盘一定要搬空了

以二路归并为例

If the number of runs is a fibonacci number \(F_N\) , then the best way to distribute them is to split them into \(F_{N-1}\) and \(F_{N-2}\)

例：\((a,b,c)\) 表示 \(T_1T_2T_3\) 中的 runs 数量

\[ \begin{aligned} &(21,13,0)\rightarrow(8,0,13)\rightarrow(0,8,5)\rightarrow\\ &(5,3,0)\rightarrow(2,0,3)\rightarrow(0,2,1)\rightarrow\\ &(1,1,0)\rightarrow(0,0,1) \end{aligned} \]

扩展到 \(k\) 路归并时

  • 定义 \(k\) 阶斐波那契数： \(F_N^{(k)} = \sum_{i=1}^k F_{N-i}^{(k)}\)
  • 按照 \(k\) 阶斐波那契数拆分更优

  • 实现方式（参考修佬的PPT）：

    • 每次 \(k\) 路归一路，取 \(k\) 路中的 min ，然后 \(k\) 路各自减去 min
    • 显而易见这样能始终保持一路为空

  • Q：如果数量不恰好为斐波那契数？

    A：在后面补上空的 runs 即可

Parallel Operation⚓︎

对于 \(k\) 路归并需要 \(2k\) 个读缓存和 2 个写缓存

（GPT对于这个2的系数的解释，以读为例：一个缓冲区正在被读取时，另一个缓冲区可以并行加载下一块数据）

  • 如果 \(k\) 增长，IO时间会增加但是 passes 会减少，buffer空间减小
  • 为达到最高效率，需要依据硬件的参数找到 trade-off 的较优解

Merge Time⚓︎

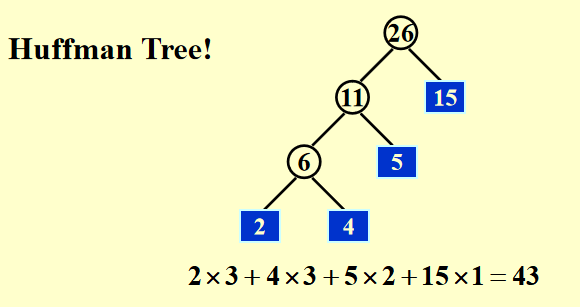
  • 利用哈夫曼编码树

例如：对四个2,4,5,15的runs作合并，如图所示的合并效率最高， \(T=O(\text{the weighted external path length})\)

image-20241229162209552