Parallel Algorithms ⚓︎

省流⚓︎

问题-算法	T	W
前缀和	\(O(\log{n})\)	\(O(n)\)
单轮归并-并行二分	\(O(\log{n})\)	\(O(n\log{n})\)
单轮归并-\(\log{n}\)分块	\(O(\log{n})\)	\(O(n)\)
找最大值-朴素并行	\(O(1)\)	\(O(n^2)\)
找最大值-\(\sqrt{n}\) 分块	\(O(\log{\log{n}})\)	\(O(n\log{\log{n}})\)
找最大值-\(\log{\log{n}}\) 分块	\(O(\log{\log{n}})\)	\(O(n)\)
找最大值-随机采样	\(O(1)\)	\(O(n)\)

\(W(n)/P(n)+T(n)\)

PRAM 模型⚓︎

特性⚓︎

假设存在多个处理器，且同时执行操作
假设所有处理器可以同时访问同一个全局的内存
假设所有处理器同步运行

运算过程⚓︎

同时读
各自计算
同时写

缺陷⚓︎

无法说明算法在不同数量处理器的实际表现
分配到处理器，过于细节繁琐而忽视算法总体架构

Work-Depth Presentation⚓︎

Work load(总操作数) W(n)
Worst-case running time T(n)

按我的理解，T(n)表征了算法中不得不品的串行部分，不包括W(n) 的并行部分

WD-presentation Sufficiency Theorem

对于一个用WD模式表示的算法，在任意的 \(P(n)\) 个处理器上需要运行 \(O(W(n)/P(n)+T(n))\) 的时间

但是要求算法遵循与WD表示法中相同的并发写入规则（没搞懂）

冲突处理规则⚓︎

EREW(Exclusive read exclusive write)：同时读或者写同一个单元都不允许
CREW(Concurrent read exclusive write)：允许同时读同一个单元，不允许同时写
CRCW(Concurrent read Concurrent write)：允许同时读和写同一个单元
- Common rule : 要求所有写入值一致否则无效
- Arbitrary rule : 随机选一个写
- Priority rule : 依据优先级选一个写（PPT上说选择编号最小的处理器的结果）

也就是

规则	同时写	同时读
EREW	✘	✘
CREW	✘	✔
CRCW	✔	✔(3 rules)

实例⚓︎

由于考试经常给一段代码让分析 \(W\) 和 \(T\) ，后面展示的代码片段最好不要直接跳过，熟悉一下并行的一些写法（例如 pardo ）

前缀和⚓︎

B(h,i) 表示第 h 层（从0开始）第 i 号节点的计算结果，成树型结构向上累加

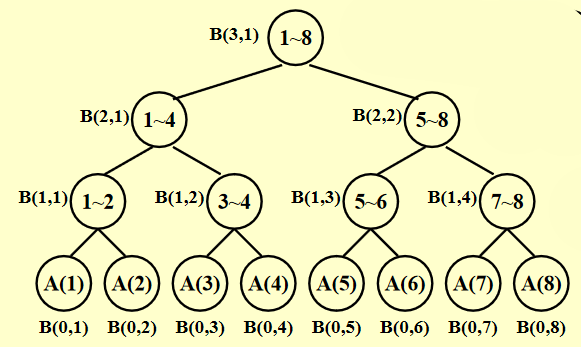
PRAM 模型⚓︎

复制数据

Code

for P_i, 1 ≤ i ≤ n pardo
    B(0, i) := A(i)

逐层向上累加

Code

for h = 1 to log n do //这层循环有层数依赖无法并行
    if i ≤ n / 2^h
        B(h, i) := B(h-1, 2i-1) + B(h-1, 2i)
    else
        stay idle

输出顶层节点

Code

for i = 1: output B(log n, 1); 
for i > 1: stay idle

WD表示⚓︎

忽略部分细节

Code

for Pi ,  1 <= i <= n  pardo
  B(0, i) := A( i )
for h = 1 to log n 
    for Pi, 1 <= i <= n/2^h  pardo
        B(h, i) := B(h-1, 2i-1) + B(h-1, 2i)
for i = 1 pardo
  output  B(log n, 1)

\(T(n)=\log{n}+2\)
\(W(n) = n+n/2+n/4+...+n/2^k+1 = 2n\)

进一步，若要求出每一个位置的前缀和，需要增加一个向下传播的过程，完整代码如下

Code

for Pi , 1 <= i <= n pardo
  B(0, i) := A(i)
for h = 1 to log n
  for i , 1 <= i <= n/2h pardo
    B(h, i) := B(h - 1, 2i - 1) + B(h - 1, 2i)
for h = log n to 0
  for i even, 1 <= i <= n/2h pardo
    C(h, i) := C(h + 1, i/2)
  for i = 1 pardo
    C(h, 1) := B(h, 1)
  for i odd, 3 <= i <= n/2h pardo
    C(h, i) := C(h + 1, (i - 1)/2) + B(h, i)
for Pi , 1 <= i <= n pardo
  Output C(0, i)

\(T(n)=O(\log{n})\)
\(W(n)=O(n)\)

归并⚓︎

将有序的A(1),...,A(n)和B(1),...B(m)合并为有序的C(1),...,C(n+m)

思路：转合并为求解排名
Rank(i,B)表示 \(A_i\) 在B中的排名，即\(B(Rank(i,B)) < A_i < B(Rank(i,B)+1)\)
Rank(i,A)表示 \(B_i\) 在A中的排名

则Merge转化为如下两步

Code

for Pi , 1 <= i <= n  pardo
    C(i + RANK(i, B)) := A(i)
for Pi , 1 <= i <= n  pardo
    C(i + RANK(i, A)) := B(i)

可以 \(O(1)\) 计算（并行），故以下讨论Rank的求法

sol 1 : 二分⚓︎

Code

for Pi , 1 <= i <= n  pardo
    RANK(i, B) := BS(A(i), B)
    RANK(i, A) := BS(B(i), A)

其中 BS 表示进行一次二分查找，这一步无法并行，因此

\(T(n)=O(\log{n})\)
\(W(n) = O(n\log{n})\)

sol 2 : 顺序计算⚓︎

Code

i = j = 0; 
while ( i <= n || j <= m ) {
    if ( A(i+1) < B(j+1) )
        RANK(++i, B) = j;
    else RANK(++j, A) = i;
}

\(T(n) = W(n) = O(n+m)\)

sol 3 : 分块处理⚓︎

前置条件：n=m，且A(n+1)与B(n+1)都大于A(n)和B(n)
则取 \(p=n/\log{n}\) ，对A和B按等间隔 \(\log{n}\) 分成 \(p\) 个块，对每个块的第一个元素先求Rank
这一步 \(T=O(\log{n})\) , \(W=O(p\log{n}) = O(n)\)
然后在两个大小为 \(\log{n}\) 的块内求每个元素的Rank，使用串行（因为这里没有办法对这 \(2\log{n}\) 个元素作并行了）
这一步 \(T=O(\log{n})\) , \(W = O(p\log{n}) = O(n)\)
综上所述，总复杂度为 \(T=O(\log{n})\) , \(W=O(n)\)

找最大值⚓︎

并行 ver0⚓︎

思路：并行比较 \(n^2\) 对数的大小关系，唯一全都大于的就是 max

for Pi , 1 <= i <= n  pardo
    B(i) := 0
for i and j, 1 <= i, j <= n  pardo
    if ( (A(i) < A(j)) || ((A(i) = A(j)) && (i < j)) )
            B(i) = 1
    else B(j) = 1
for Pi , 1 <= i <= n  pardo
    if B(i) == 0
       A(i) is a maximum in A

使用CRCW-Arbitrary rule
\(T(n)=O(1)\)
\(W(n) = n^2\)

Doubly-logarithmic Paradigm⚓︎

若按照 \(\sqrt{n}\) 分块
- 对于每个块，使用上述的ver 0求解 max 得到 \(\{M_i\}\) ，（并行执行），\(T=T(\sqrt{n}) = O(1)\) \(W=W(\sqrt{n}) = O(n)\)
- 然后对 \({M_i}\) 再做同样的操作（按根号分块，聚合，如此反复）
- 一共要执行 \(n=2^{2^h}\) 的 \(h\) ，即 \(\log{\log{n}}\) 次
- 故 \(T = O(\log{\log{n}})\) , \(W=O(n\log{\log{n}})\)
若按照 \(h=\log{\log{n}}\) 的大小分块，总组数 \(n/h\)
- 同上述操作进行，共进行 \(\log{\log{(n/h)}}\) 次递归
- \(T = O(h+\log{\log{(n/h)}}) = O(\log{\log{n}})\) \(W=O(h\times(n/h)+(n/h)\log{\log{(n/h)}})=O(n)\)
- 理解这里多出来的h和h*n/h从何而来（目前猜测第一层使用了直接的线性求解max）

随机采样Random Sampling⚓︎

高可能性（但不是一定）失败概率 \(O(1/n^c)\)，c是一个正常数
T(n) = O(1) , W(n)=O(n)

步骤：

\(n^{1/8}\) 中随机取样，得到 \(n^{7/8}\) 个元素
\(T=O(1),W=O(n^{7/8})\)
将这 \(n^{7/8}\) 个元素再按 \(n^{1/8}\) 为单位分块，一共就 \(n^{3/4}\) 块；每个 \(n^{1/8}\) 块取最大值
\(T=O(1),W=O(n^{3/4}×n^{2×1/8})=O(n)\)
现在剩下\(n^{3/4}\) 个元素，按\(n^{1/4}\) 为单位分块，共计 \(n^{1/2}\) 个块；每个 \(n^{1/4}\)取最大值
\(T=O(1),W=O(n^{1/2}×n^{2×1/4})=O(n)\)
剩下 \(n^{1/2}\) 个元素，直接取最大值
\(T=O(1),W=O(n^{2×1/2})=O(n)\)

作业⚓︎

T1

判断：In order to solve the maximum finding problem by a parallel algorithm with T(n)=O(1) , we need work load \(W(n)=Ω(n^2)\) in return.

Answer

F

ver0确实需要 \(W(n)=O(n^2)\) ，但是随机采样不是，认为随机采样可以解决问题（实在不行多跑几次）

以下的另外一道题就是正确的表述

To solve the Maximum Finding problem with parallel Random Sampling method, O(n) processors are required to get T(n)=O(1) and W(n)=O(n) with very high probability.

T2

The prefix-min problem is to find for each i, 1≤i≤n, the smallest element among A(1), A(2), ⋯, A(i). What is the run time and work load for the following algorithm?

Code

for i, 1≤i≤n pardo
  B(0, i) = A(i)
for h=1 to log(n)
  for i, 1≤i≤n/2^h pardo
    B(h, i) = min {B(h-1, 2i-1), B(h-1, 2i)}
for h=log(n) to 0
  for i even, 1≤i≤n/2^h pardo
    C(h, i) = C(h+1, i/2)
  for i=1 pardo
    C(h, 1) = B(h, 1)
  for i odd, 3≤i≤n/2^h pardo
    C(h, i) = min {C(h + 1, (i - 1)/2), B(h, i)}
for i, 1≤i≤n pardo
  Output C(0, i)

Answer

答案： \(T=O(\log{n})\) , \(W=O(n)\)

分析同前缀和部分 ~~这道题题面写的lofn我真的会笑死~~

Parallel Algorithms⚓︎

省流⚓︎

PRAM 模型⚓︎

特性⚓︎

运算过程⚓︎

缺陷⚓︎

Work-Depth Presentation⚓︎

冲突处理规则⚓︎

实例⚓︎

前缀和⚓︎

PRAM 模型⚓︎

WD表示⚓︎

归并⚓︎

sol 1 : 二分⚓︎

sol 2 : 顺序计算⚓︎

sol 3 : 分块处理⚓︎

找最大值⚓︎

并行 ver0⚓︎

Doubly-logarithmic Paradigm⚓︎

随机采样Random Sampling⚓︎

作业⚓︎

Parallel Algorithms ⚓︎