跳转至

分治算法⚓︎

这个算法在之前讲归并排序的时候就已经涉及，在本课程中的重点是主定理

主定理⚓︎

一些数学推导基础

  • \(a^{\log_b{N}} = a^{\frac{\log_a{N}}{\log_a{b}}}=N^{\log_b{a}}\)
  • 对 \(T(N) = aT(N/b)+f(N)\) 进行展开
\[ \begin{aligned} T(N) &= aT(N/b)+f(N)\\ &=a(aT(N/b^2)+f(N/b))+f(N)\\ &=...\\ &=a^kT(N/b^k)+\sum_{i=0}^{k-1} a^if(N/b^i) ,其中 k=\log_b{N}\\ &=N^{log_b{a}}+\sum_{i=0}^{k-1} a^if(N/b^i) \end{aligned} \]

对这个式子的两个观察结果：

  • 若后面那坨东西复杂度不高于 \(N^{log_b{a}}\) ，则总复杂度就是 \(\Theta(N^{log_b{a}})\)

  • 一个重要的临界是 \(f(N) = N^{log_b{a}}\) ，这意味着 \(a^if(N/b^i)\) 与 \(f(N)\) 等同，后面的级数和大致是 \(f(N)log_b{N}\) 。

形式1⚓︎

对于 \(T(N) = aT(N/b) + f(N)\)

  • 若\(\exists\) \(\varepsilon > 0\) 使得 \(f(N) = O(N^{log_b^{a}-\varepsilon})\) ，则 \(T(N) = \Theta(N^{log_b{a}})\)
  • 若 \(f(N) = \Theta(N^{log_b{a}})\) ，则 \(T(N) = \Theta(N^{log_b^a}\log{N})\)
  • 若\(\exists\) \(\varepsilon > 0\) 使得 \(f(N) = \Omega(N^{log_b{a}-\varepsilon})\) ，且存在常数 \(c<1\) 使得 \(af(N/b)<cf(N)\) ，则 \(T(N) = \Theta(f(N))\)

形式2⚓︎

对于 \(T(N) = aT(N/b) + f(N)\)

  • 若\(\exists \kappa<1\) 使得 \(af(N/b) = \kappa f(N)\) ，则 \(T(N) = \Theta(f(N))\)
  • 若 \(af(N/b) = f(N)\) ，则 \(T(N) = \Theta(f(N)\log_b{N})\)
  • 若\(\exists K > 1\) 使得 \(af(N/b) = K f(N)\) ，则 $T(N) = \Theta(N^{log_b{a}}) $

前两个形式具有高度的相似性。考虑我们在公式推导时发现的临界点 \(f(N) = N^{log_b{a}} \Leftrightarrow af(N/b)=f(N)\) ，这两个形式都是基于这一临界进行讨论，从而确定 \(N^{log_b{a}}\) 与 \(\sum_{i=0}^{k-1} a^if(N/b^i)\) 哪一项占据主导，这也是它为何被称为主定理。

形式3⚓︎

对于 \(T(N) = aT(N/b) + \Theta(N^k\log^p{N})\) \((a\ge 1,b>1,p\ge 0)\)

\[ T(N) = \begin{cases} O(N^{\log_b{a}}) & \text{if } a > b^k, \\ O(N^k \log^{p+1} N) & \text{if } a = b^k, \\ O(N^k \log^p N) & \text{if } a < b^k \end{cases} \]

案例: Closet Points Problem⚓︎

Given N points in a plane. Find the closest pair of points. (If two points have the same position, then that pair is the closest with distance 0.)

考虑将整个平面一分为二，则最近点对的构成为：

  • 单侧平面内部的点对
  • 跨越分割线的点对

由此进行分治，现在我们只需考虑如何处理跨越分割线的点对。

暴力做法的复杂度是 \(O(N^2)\) ，若要使复杂度有所优化， \(f(N)\) 不能达到 \(O(N^2)\) ，例如当 \(f(N)=\Theta(N)\) 时总复杂度为 \(O(N\log{N})\) 。

在处理跨越分界线的点对时，我们仍然采用暴力解法，这意味着我们需要将候选点的规模降低，例如到 \(O(\sqrt{N})\) ，但是这是不太容易的，因此我们需要同时从降低节点规模和优化枚举方式两方面推进。

假设分割线是竖直的，一个直白的思路是利用分治求得两边最近点对的距离最小值 \(\delta\) ，当点到分割线的距离都大于 \(\delta\) 时，这个点就不可能对答案有贡献。

img1

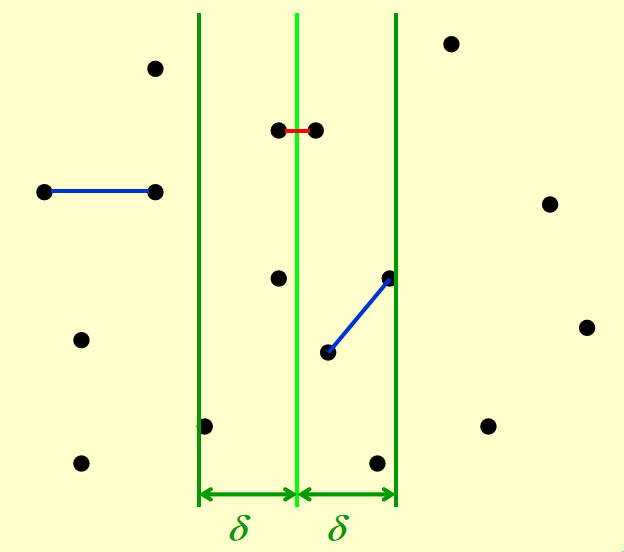
刚刚这个限制只限制了横坐标，同样的思路在确定到单个节点时同样可以作用于纵坐标，即如果当前枚举的左侧节点纵坐标为 \(y\) ，那么右侧只需要枚举纵坐标在 \([y-\delta,y+\delta]\) 的点。为了便于使用 two pointers 的技巧进行线性枚举，可以从左侧和右侧都枚举一次，从而每个点枚举都只考虑与纵坐标不小于自己的点组合，即对每个点存在一个 \([2\delta\times\delta]\) 的搜索框。

值得注意的是，由于这个 \(\delta\) 的来源是 "两边最近点对的距离最小值" ，在同侧的点与正在考虑的点的距离都不会小于 \(\delta\) ，因此这个搜索框在极端条件下（同侧卡住 \(\delta\) 界限，且节点跨越分界线）也只存在包括自己在内的八个点。

img2

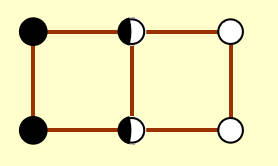
综上，可以做到 \(f(N)=O(N)\) 。