回溯算法⚓︎

回溯模板

bool Backtracking ( int i ){
    Found = false;
    if ( i > N )return true; /* solved with (x1, ..., xN) */
    for ( each xi in Si ) { 
        /* check if satisfies the restriction R */
        OK = Check((x1, ..., xi) , R ); 
        /* pruning */
        if ( OK ) {
            Count xi in;
            Found = Backtracking( i+1 );
            if ( !Found )Undo( i ); 
            /* recover to (x1, ..., xi-1) */
        }
        if ( Found ) break; 
    }
    return Found;
}

考虑对称性可以少算不少

案例⚓︎

Turnpike Reconstruction Problem⚓︎

Given $N$ points on the x-axis with coordinates $x_1 < x_2 < …< x_N $ . Assume that $x_1 = 0$. There are $N ( N – 1 ) / 2$ distances between every pair of points. Given $N ( N – 1 ) / 2$ distances. Reconstruct a point set from the distances.

解题过程：

通过给出的 distances 的数量确定 $N$ 的大小。
将 distances 数组从大到小观察：

毫无疑问最长的距离必定对应 $x_0$ 到 $x_N$ 的距离，从而可以敲定 $x_N$ 的坐标。

此时次长的距离存在两种可能： $x_0$ 到 $x_{N-1}$ 或者 $x_1$ 到 $x_N$ ，据此分别进行搜索。

值得注意的是，第 $i$ 个被确认的坐标会为当前局面增加 $i$ 段距离（假设 $x_N$ 是第一个被确认的），此时需要与已知条件对照，以免在不合法分支中浪费时间。

Tic-tac-toe⚓︎

对于两个理性人的三子棋对弈，双方在操作时都会选择让对方后续局面最不利的操作，同时由于对面也是理性人，他也会选择让本方最不利的局面。

对于先手 $A$ 和后手 $B$ 的对弈，我们可以设计一个函数来粗略反应局势对 $A$ 的有利程度：

\[ f(P)=W_A-W_B \]

其中 $W_x$ 指当前局面下 $x$ 方可能的获胜情形（不考虑另一方的操作，可以简单理解成剩下空地全部填满自己的棋子之后有多少个不同的三连。）

那么 $A$ 方总是会选择最大化 $f(P)$ 的分支，而 $B$ 方选择将其最小化。PPT上称其为 Minimax Strategy ，表现在搜索树上呈现为一层取 min 一层取 max 的状态。

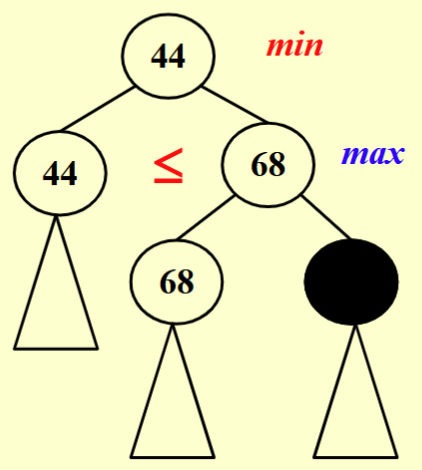
针对这个搜索树，有一种剪枝技巧叫 $\alpha-\beta$ pruning，具体来说包含 $\alpha$ 和 $\beta$ 两种剪枝方式：

$\alpha$ pruning ：在求 max 的层向下搜索（则本层是取min），如果计算出比当前解更小的解就无需再搜索

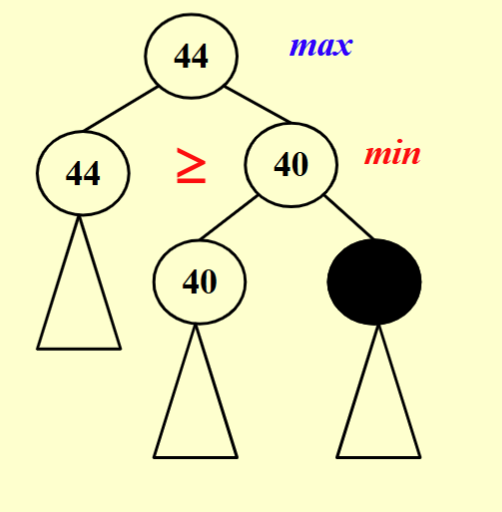
$\beta$ pruning ：在求 min 的层向下搜索（则本层取max），若计算出比当前已知解更大的解就无需再搜索