二项队列⚓︎

二项队列与二项树

二项队列不是二叉树，而是是一些二项树组成的集合，也就是说，它其实是一个森林。

二项队列也被叫做二项堆，但是正如上面所说它实质上是一个森林，跟之前我们所学的那些单棵二叉树的堆都不太一样，所以在行文中我也会用“二项队列”这个说法来强调这一点。

而二项树的定义是递归式的：

首先，我们称单个的节点是 0 阶的二项树，

而一棵 \(k\) 阶的二叉树（记作 \(B_k\) ）则由两棵 \(B_{k-1}\) 将根节点相连形成。

下图是从 0 阶到 3 阶的二项树

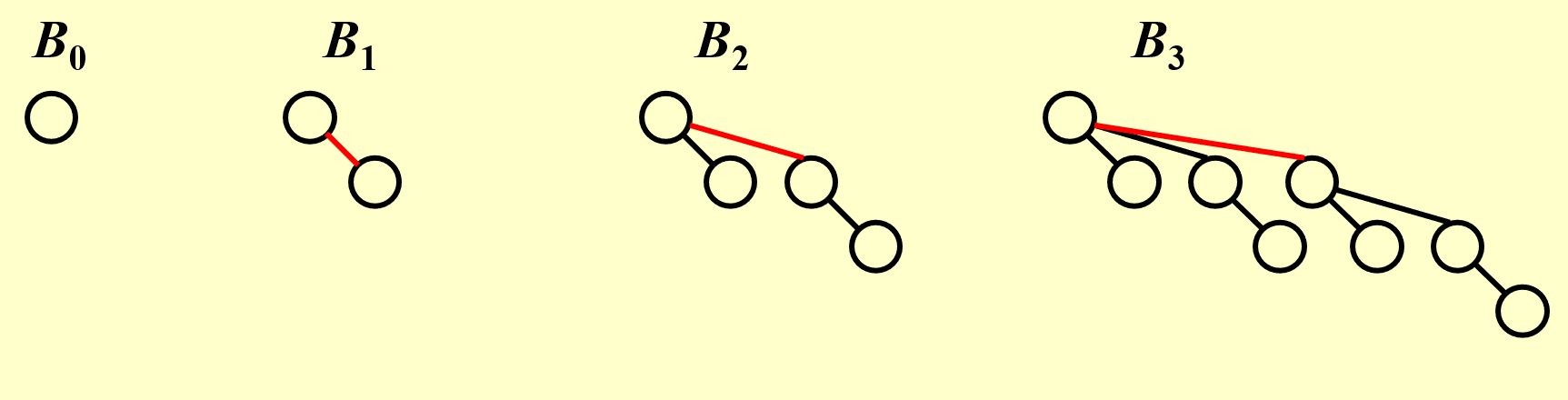
通过观察图片找规律或者数学推导可以得出如下性质：

\(B_k\) 共有 \(2^k\) 个节点，深度为 \(i\) 的一层（根深度为 0 ）有 \((^k_i)\) 个

在一个二项队列中，同一阶的二项树至多出现 1 棵，否则将这两棵树连接在一起即可变为一个高一阶的树。

这一性质可以很自然地与二进制数的表示联系在一起，因而通过整个二项队列的总结点数量可以唯一的确定它包含哪些阶的二项树。

操作⚓︎

（代码来自课堂PPT）

结构体定义

typedef struct BinNode *Position;
typedef struct Collection *BinQueue;
typedef struct BinNode *BinTree;
struct BinNode
{
    ElementType Element;
    Position LeftChild;
    Position NextSibling;
};
struct Collection
{
    int CurrentSize;
    BinTree TheTrees[MaxTrees];
};

Merge⚓︎

我们前文说每个二项队列与其总结点数的二进制表示紧密联系，此处两个二项队列的合并也是如此，整个过程与二进制数的加法近乎于同步。

我们首先需要完成一个一位的加法器，放在这里就是处理两棵同阶的二项树的合并，它的实现是非常简单且显然的。

Code

BinTree CombineTrees( BinTree T1, BinTree T2 )
{
    if(T1->Element > T2->Element) return CombineTrees(T2,T1);
    T2->NextSibling = T1->LeftChild;
    T1->LeftChild = T2;
    return T1;
}

从这里也能看出来，一个节点的儿子是按照子树大小降序排列的,因为最新接入成为 LeftChild 的是一棵与本树原本阶数相同的树，而不会再有比这更大的子树了。

从这到整个队列的合并，非常类似于从半加器到全加器，在单独考虑每一位的时候都引入了对进位的考虑，从低到高计算。

Code

BinQueue Merge( BinQueue H1, BinQueue H2 )
{
    BinTree T1,T2,Carry = NULL;
    int i,j;
    if( H1->CurrentSize + H2->CurrentSize > Capacity ) ErrorMessage();
    H1->CurrentSize += H2->CurrentSize;
    for( i = 0; j = 1; j <= H1->CurrentSize; ++i, j *= 2){
        T1 = H1->TheTrees[i];
        T2 = H2->TheTrees[i];
        switch(4*!!Carry + 2*!!T2 + !!T1){
            /*
            对这个switch语句进行一点解释
            1. !!Carry
                通过两次取反得到一个布尔值，表示这个指针是否为空
            2. 4**!!Carry+ 2*!!T2 + !!T1
                将这三个指针是否为空的情况映射到一个三位二进制数，方便确定到底哪一个为空
                （因为二进制中的1是等价的，但是这里的三棵树不是完全等价的）
            */
            case 0:case 1:break;
            case 2: H1->TheTrees[i] = T2;
                    H2->TheTrees[i] = NULL;break;
            case 4: H1->TheTrees[i] = Carry;
                    Carry = NULL;break;
            case 3: Carry = CombineTrees( T1, T2 );
                    H1->TheTrees[i] = H2->TheTrees[i] = NULL;break;
            case 5: Carry = CombineTrees( T1, Carry );
                    H1->TheTrees[i] = NULL;break;
            case 6: Carry = CombineTrees( T2, Carry );
                    H2->TheTrees[i] = NULL; break;
            case 7: H1->TheTrees[i] = Carry; 
                    Carry = CombineTrees( T1, T2 ); 
                    H2->TheTrees[i] = NULL; break;
        }
    }
    return H1;
}

单次复杂度 \(O(\log n)\) ，均摊 \(O(1)\) ，将在后文具体分析

DeleteMin⚓︎

单棵树保证根节点最小（详见前文的 Merge 实现），但是整个队列有多棵树，因此需要遍历根节点列表并找到最小。（或者对此进行维护）

对于删除，将最小根节点取出，将其对应二项树拆成所有子树再Merge回去。

整个操作 \(O(\log n)\)

Code

ElementType  DeleteMin( BinQueue H )
{   
    BinQueue DeletedQueue; 
    Position DeletedTree, OldRoot;
    ElementType MinItem = Infinity;
    int i, j, MinTree;
    if ( IsEmpty( H ) )  {  PrintErrorMessage();  return –Infinity; }
    for ( i = 0; i < MaxTrees; i++) {
        if( H->TheTrees[i] && H->TheTrees[i]->Element < MinItem ) { 
            MinItem = H->TheTrees[i]->Element;  MinTree = i;            } 
    } /* end for-i-loop */
    DeletedTree = H->TheTrees[ MinTree ];  
    H->TheTrees[ MinTree ] = NULL;
    OldRoot = DeletedTree; 
    DeletedTree = DeletedTree->LeftChild;   
    free(OldRoot);
    DeletedQueue = Initialize();    
    DeletedQueue->CurrentSize = ( 1<<MinTree ) – 1;  
    for ( j = MinTree – 1; j >= 0; j – – ) {  
        DeletedQueue->TheTrees[j] = DeletedTree;
        DeletedTree = DeletedTree->NextSibling;
        DeletedQueue->TheTrees[j]->NextSibling = NULL;
    }
    H->CurrentSize  – = DeletedQueue->CurrentSize + 1;
    H = Merge( H, DeletedQueue );
    return MinItem;
}

其他操作⚓︎

Find-Min : 在根节点队列中遍历寻找 \(O(\log{n})\) 但是如果专门记录更新可以做到 \(O(1)\)
Insert：即将一棵 \(B_0\) 树合并到队列中，单次最好 \(O(1)\) 最坏 \(O(\log n)\) ，均摊 \(O(1)\)
Build：将节点逐个插入，由均摊分析得总复杂度 \(O(n)\)
Decrease Key：在二叉树上进行上调，显然 \(O(\log n)\)

均摊分析⚓︎

考虑建二项队列的过程。整个过程就是向现存队列中不断插入一个 \(B_0\) 。

那些复杂度特别高的情况都是引发多次合并的情况，继续类比二进制数的话就是连续进位。为了通过均摊分析把这种连续进位的不确定性抵消掉，势能函数应当表现出来这种合并的变化。

因此我们选择 \(\varPhi = \text{number of trees}\) 。从直觉的角度来看，多次的进位必然导致相同数量的树被合并掉，最后保留常数的 \(\hat{c_i}\) 。

具体来说，假设进行插入时现有单独的树\(B_0,B_1,...,B_k, B_{k+t},....(t\ge 2)\)，

则插入时会与 \(B_0\) 到 \(B_k\) 合并得到一棵 \(B_{k+1}\) ，其他不变，

则 \(\Phi_i - \Phi_{i-1} = -k\) （正在插入的那个点也是一棵树）

\[ \hat{c_i} = c_i + \Phi_i - \Phi_{i-1} = 1+(k+1) -k = 2 \]

其中 \(c_i\) 的构成为 \(k+1\) 次合并和 1 的节点创建

如果使用 Accounting Method ，可以这样想：

每个点初始一块钱，每次合并两棵树的操作花掉成为子树的那棵树的一块钱，则整个树至少还有一块钱（在根节点上），则整个系统钱不会为负，因而总复杂度是 \(O(N)\) 的

进一步的，由建树的过程可以得到每个点的插入平均下来也是 \(O(1)\) 的。