斜堆⚓︎

与左偏树的实现大同小异，但是无需维护 Npl 。按照题目中的说法，它和 splay 都属于 "self adjusting data structures" 。

具体来说，相较于左偏树仅在不满足左偏性质时交换左右儿子，斜堆在递归路径上的每个父节点都会在合并后交换左右儿子。

Code

//实现细节上可能与老师有点差异？
newnode(int v){//返回节点编号     
    int x=++cnt;    
    val[x]=v,ls[x]=rs[x]=0;     
    return x; 
} 
int merge(int a,int b){//以a,b为根的树合并,返回根节点   
    if(!a||!b) return a+b;
    if(val[a] > val[b]) swap(a,b);  
    rs[a]=merge(rs[a],b);   
    swap(ls[a],rs[a]);
    return a; 
}

复杂度分析⚓︎

轻节点与重节点

称一个节点为 heavy node ，当且仅当它满足“右子树大于左子树”这一条件，反之称其为 light node 。

更准确的说法如下

A node p is heavy if the number of descendants of p’s right subtree is at least half of the number of descendants of p, and light otherwise. Note that the number of descendants of a node includes the node itself.

性质

除了归并路径上的节点，其他节点轻重性质不发生改变
归并后，重节点一定变轻，但是轻节点不一定变重

解释

因为整个归并路径上的节点的右子树大小必然增加，然后进行左右交换。

原来右子树就比左子树大的重节点在右子树大小增加后此关系不改变，因此交换左右子树后必然左子树更大，

然而轻节点就不一定，要视 merge 的树的大小决定。
整棵树最右侧链上的轻节点数量是 \(O(\log{n})\) 的

解释

当这条链上的轻节点数量越多，那么树的结构就越趋近于左偏树，并导致这条链的长度越短，最终整条链长度达到 \(O(\log{n})\)

令 \(D_i\) 为第 \(i\) 次操作后的根节点，势能函数为 \(\Phi (D_i) = \text{number of heavy nodes}\)

假设最开始的右路径（即归并路线）上轻节点 \(l_i\) ，重节点 \(h_i\) 。

那么最极端情况轻节点全部变成重节点

\[ \begin{aligned} T_{worst}&=l_1+h_1+l_2+h_2\\ \varPhi_i &= h_1+h_2+h\\ \varPhi_{i+1} &\le l_1+l_2+h\\ T_{amortized} &= T_{worst}+\phi_{i+1}-\phi_i\le 2(l_1+l_2) \Rightarrow O(\log N) \end{aligned} \]

作业⚓︎

直接把部分结论列出来好了

按顺序插入 \(1-2^k-1\) 得到的总是完全满二叉树
斜堆的 right path 长度是任意的，只是轻节点数受到限制

斜堆合并

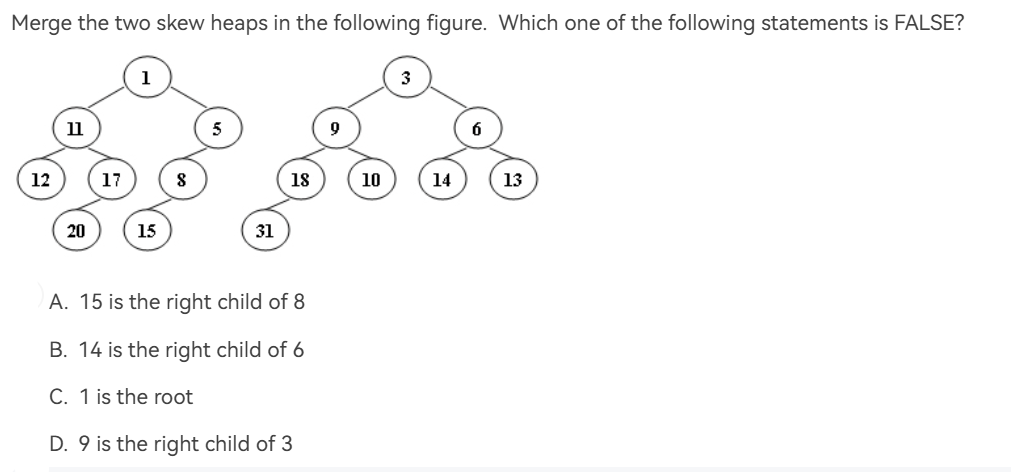
Answer

A

斜堆⚓︎

复杂度分析⚓︎

作业⚓︎

评论