跳转至

红黑树⚓︎

合法红黑树的5个性质

一棵合法的红黑树需要满足如下条件：

  • 节点分为红黑两种颜色

  • 根节点为黑色

  • 空节点（NIL）为黑色

  • 红色节点的子节点一定为黑色

  • 从根节点往下到叶节点（NIL），每条路径上黑色节点数量相同

  • 定义每个节点的黑高 (Black height)是从自己向下到NIL的路径上黑色节点的个数（但是不包含自己）

    • 例如 BH(NIL) = 0， 单个节点的树 BH = 1（对应NIL，根节点本身不算在内）
内部节点和外部节点

External node指NIL，其他有值的都是Internal node

性质

  • 可以得到的导出性质（用于判别红黑树）：红黑树的红色节点的两个子节点一定同为叶子或同不为叶子（其中叶子指NIL）。
证明

首先红色节点的子节点必然是黑色的。

若两个子节点一个是 NIL 一个不是，非叶子节点往下至少还有一个 NIL，则这两条路径黑高不等。

  • \(N\) 个内部节点（不含NIL）的红黑树的高度最大为 \(2\log_2(N+1)\)
证明

综合以下两条

\[ \begin{cases} N \ge 2^{BH} - 1\\ Height \le 2BH \end{cases} \]

操作⚓︎

  • Rotate : 与 AVL 的旋转操作基本一致，不再赘述

Insert⚓︎

  • 思路为先以红色节点的形式像普通 BST 一样插在叶节点（因为会有两个 NIL 所有肯定满足性质4，且插入红色节点不影响黑高），然后再调整使得红色节点不相邻。记插入节点为 x

  • 若 x.fa 是黑色就不用调整

  • 若 x.fa 是红色，需要分类讨论并且向上递归处理。下图中橘色节点代表使红黑树失衡的子树

    • case 1：将两个红色节点染黑，“根节点”染红，并向上递归处理（引号是因为是当前考虑的子树的根而不一定是整颗树的）

    • 如果"根节点"没有父亲，则根节点再染黑，结束

    • 如果”根节点“的父亲是黑，直接结束

    • 如果根节点父亲是红的，向上递归，可能转成其他case

    • case 2 : 基于橙色节点左旋转为 case 3

    • case 3 : 红色节点染黑，其父亲染红，再将新的黑色节点右旋上去。个人理解思路为将红色节点分给右侧

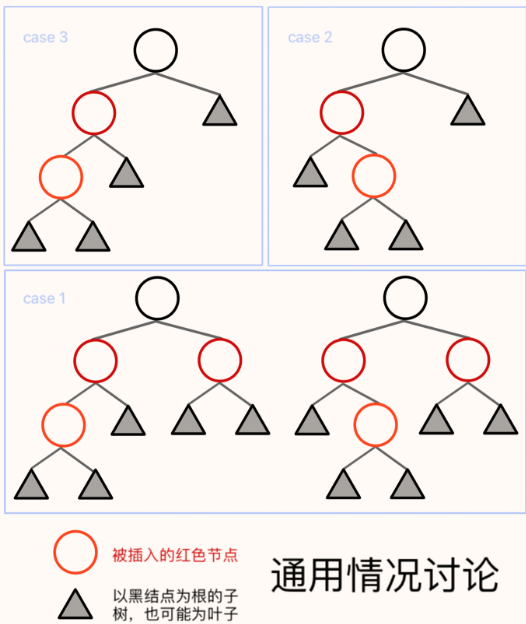
    Insert

    • 综合上述情况，只有case1可能向上递归，其他情况不会。只有case2 和 case3 需要 Rotate ，因此最多旋转次数为从 case2 转到 case3 ，即最多两次

  • 复杂度 \(O(\log{n})\)

Delete⚓︎

赞美修佬

  • 考虑分成两部分进行分类讨论：删除和删除后平衡维护

  • 删除

  • case 0 : 如果整颗树只有一个节点直接删，无需后续维护（可以理解为特化的 case 3 ? ）

  • case 1 : 如果该节点左右儿子都有就取前驱/后继（只取值不取颜色）代替自己并删除前驱/后继对应节点，前驱/后继可能是没有儿子的，这种情况即转为 case 3 ，也可能是只有一个儿子的，这种情况即转为 case 2

  • case 2 : 如果该节点左右儿子只有一个，则那个节点一定是红的（因为黑高一致），则本节点一定是黑的。用子节点代替待删除节点并染黑即可，无需后续维护

  • case 3 : 如果该节点没有（非空）子节点，若节点为红直接删掉，节点为黑删掉后还要维护一下

结论 每个 case 都能转化为删除叶节点的情况，但只有在最后转化为删除某黑色节点时才会导致黑高的性质不能满足，需要进行平衡维护。

  • 平衡维护：也需要递归地调整。记当前导致失衡的子树的根节点是x（颜色不定） ，依据兄弟节点(w)、其子节点(lc & rc)以及父亲节点(fa)进行分类。以下以 x 为左子树为例，右子树则需对称处理。

  • case 1 : w , lc , rc 全黑

    • case 1.1 fa 是红色的：将 w 染红， fa 染黑，相当于从 w 子树中抽一个黑色出来共享给 x

    • case 1.2 fa 是黑色的：同样将 w 染红，然而在 fa 的子树内无法找到可以用来从红转黑共享给 x 的黑色节点，因而将矛盾转移到 fa 以上的部分。如果 fa 就是根节点，则可以直接退出（因为整棵树黑高平等减一）。

  • case 2 : w 黑，rc 红：将 w 染为和 fa 相同的颜色，将 rc 和 fa 染黑，并对 fa 进行一次左旋。思路是给 x 上方补一个黑节点，为了和其他子树保持一致顶上留一个与原 fa 相同的节点。因为 rc 的高度-1，将 rc 本身变黑以弥补。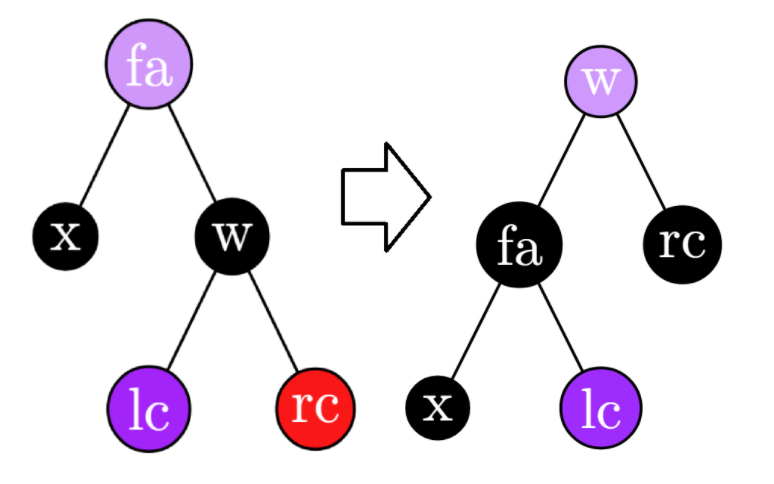

    case2

  • case 3 : w , rc 黑，lc 红：刚刚那个思路中更改 rc 颜色用于补偿的步骤无法实施。将 w 染红， lc 染黑，右旋 w 使得 lc 成为新的根。可以发现在 w 和 lc 对调染色时， lc 的整体黑高比 rc 高了 1，其左右两子树的黑高倒是与 rc 一致，因此将 lc 转到根节点后 lc 子树内黑高与原先一致，但右子节点变红了，则状况转为 case 2 。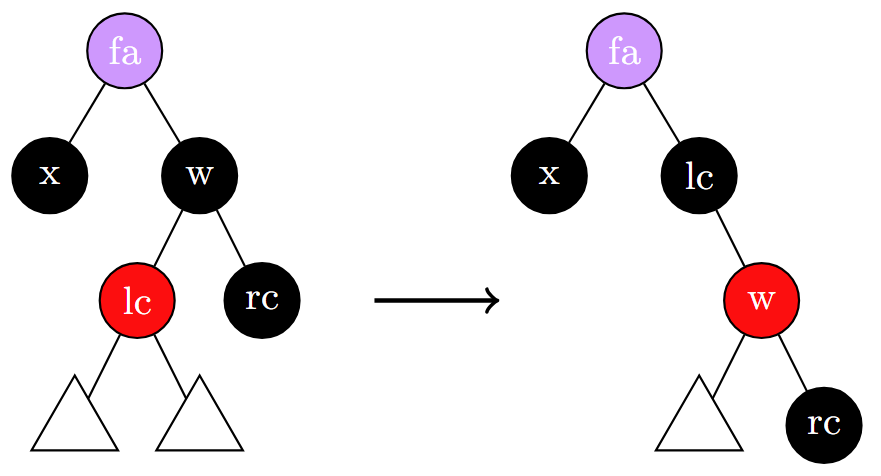

    case3

  • case 4 : fa , lc , rc 黑， w 红：将 fa 左旋，使 w 成为新的根节点。但此时左右两子树黑高差1，因此将 fa 染红， w 染黑（此时至少保证了向 lc 方向的路径与向 rc 方向的路径黑高一致），然而 fa 子树内黑高仍然不相等，因此递归到子树中去，可能转化为 case 1.1,case 2,case 3。

​ 懒得画了，借一下oiwiki的图

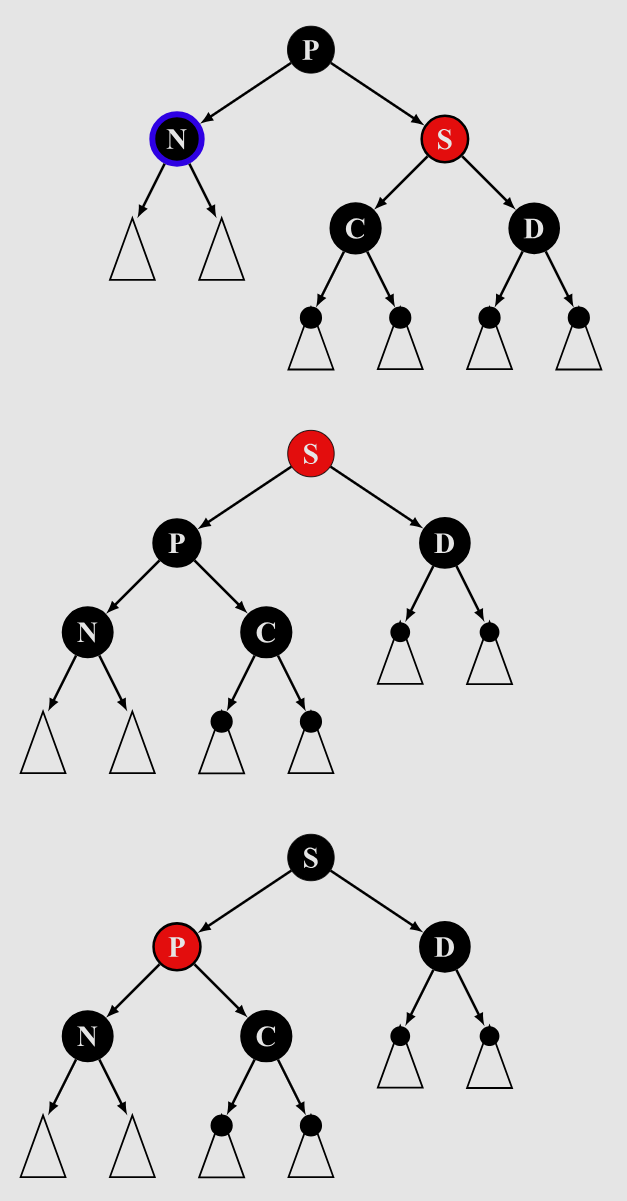
case4

  • 综合以上四种情况：case1.2需要向上递归，case4需要向下递归，剩余情况无需递归。case2，case3，case4中存在Rotate操作，则最多旋转次数为由 case4 转到 case3 再到 case2 ，共计3次

  • 删除部分最坏即寻找前驱后继，复杂度为树高；平衡维护部分向上递归 (case1.2) 与向下递归 (case4) 不兼容，因此最坏复杂度即树高， \(O(\log{n})\)

  • 查找前驱后继等操作同正常 BST

比较：AVL与RBT的旋转操作次数⚓︎

AVL RBT
Insert \(\le 2\) \(\le 2\)
Delete \(O(\log{n})\) \(\le 3\)

分析见AVL和红黑树的相应部分。

作业题⚓︎

T1：插入节点

T1

Tip

得到结果19是红色的

T2：删除节点（但是强度很低）

T2

Tip

谁顶上去谁变黑

评论