B+树⚓︎
是一种多叉树
定义
A B+ tree of order M is a tree with following structural properties:
- Root: a leaf / has [2~M] children
- Nonleaf nodes (except root) : has [\(\lceil M/2 \rceil\) , M] children
- Leaf: same depth
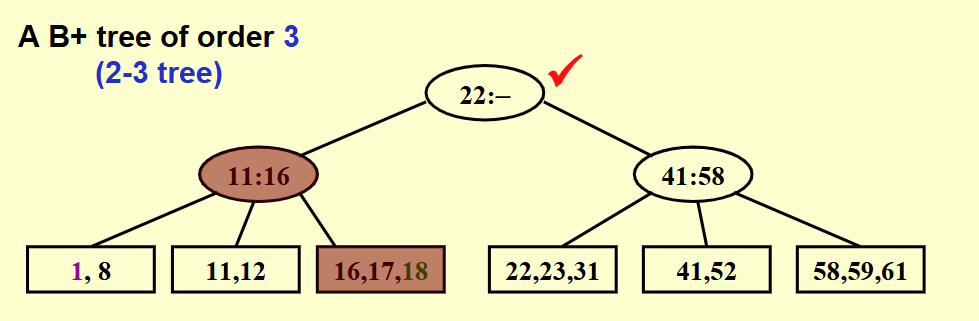
如图为 M = 3 的情况
可以看出非叶子节点最多存储 M-1 个键值,其中第 i 个对应其第 i+1 个子树中存储的最小值
操作⚓︎
Find⚓︎
-
与当前节点的所有子节点左边界值进行比较以找到应该在的区间,从而递归入相应子节点进行查找
-
如果不使用二分查找优化复杂度 \(O((M/\log{M})\log{N})\) ,否则 \(O(\log{N})\) 。 Insert 和 Delete 操作同理。
Code
Node Find(int key, Node cur){
int i = 0;
while( i < cur.cntSon )
if(key >= cur.keys[i] ) ++i;
if( i == cur.cntkeys ) return EmptyNode;
return Find(key, cur.son[i]);
}
Insert⚓︎
先递归到对应的区间,即叶节点,此时有几种情况:
-
如果那个区间包含的数不超过 M - 1 个:直接插入进去就行
-
否则,需要对这个区间进行分裂,上层结构也需要有相应变化
-
当前叶节点分裂成两个,各自拥有 \(\lfloor (M+1)/2 \rfloor\) 个数
-
递归处理父节点,直到找到一个儿子数量没到 \(M-1\) 的祖宗节点为止。如果直到根节点都不满足要求,重新建一个根节点并将原根节点分裂
-
下面给出一个大框架
沿着链向上处理分裂
void deal(int cur, int son0, int son1, int insert_val){
if(!cur){
Set(cur = root = ++cnt, 2, 1, 0);
UpdateRelation(cur, son0, son1);
T[cur].v[0] = insert_val;
T[cur].fa = 0;
return;
}
//处理掉父亲关系问题
if(T[cur].totv < 2){
InsData(T[cur].v, T[cur].v, &T[cur].totv, insert_val);
int pos;
for(pos = T[cur].totch; pos; --pos){
if(T[cur].ch[pos - 1] == son0){
T[cur].ch[pos] = son1;
break;
}
T[cur].ch[pos] = T[cur].ch[pos - 1];
}
T[cur].totch++;
T[son1].fa = cur;
return;
}
// 分裂示意图
// / \(v2)
// cur(v1~v3) cur(v1) newnode(v3)
// / | \ =>; / \ / \
// A son B A son0 son1 B
//
InsData(T[cur].v, b, &T[cur].totv, insert_val);
Set(++cnt, 2, 1, 0);
T[cnt].v[0] = b[2];
Set(cur, 2, 1, 0);
T[cur].v[0] = b[0];
if(T[cur].ch[0] == son0) {
UpdateRelation(cnt, T[cur].ch[1], T[cur].ch[2]);
UpdateRelation(cur, son0, son1);
}
else if(T[cur].ch[1] == son0) {
UpdateRelation(cnt, son1, T[cur].ch[2]);
UpdateRelation(cur, T[cur].ch[0], son0);
}
else UpdateRelation(cnt, son0, son1);
deal(T[cur].fa, cur, cnt, b[1]);
}
插入操作
int Insert(int cur, int val){
if(T[cur].IsLeaf){
if(Check(T[cur], val)) return 0;
if(T[cur].totv < 3){
InsData(T[cur].v, T[cur].v, &T[cur].totv, val);
}
else{
InsData(T[cur].v, b, &T[cur].totv, val);
Set(++cnt, 0, 2, 1);
Set(cur, 0, 2, 1);
for(int i = 0; i < 2; ++i){
T[cur].v[i] = b[i];
T[cnt].v[i] = b[2+i];
}
if(T[cur].fa)
deal(T[cur].fa, cur, cnt, b[2]);
else{
Set(root = ++cnt, 2, 1, 0);
T[root].v[0] = b[2];
T[root].fa = 0;
UpdateRelation(root, cur, cnt - 1);
}
}
return 1;
}
int to_node = 0;
for(int i = 0; i <= T[cur].totv; ++i)
if(val >= T[cur].v[i]) ++to_node;
return Insert(T[cur].ch[to_node], val);
}
Delete⚓︎
- 同样是递归到相应叶节点进行处理
- 当删除掉当前值不会使叶节点包含值少于 \(\lceil M/2 \rceil\) ,直接删除
- 若删除后本节点不符合要求
- 若兄弟节点包含多于 \(\lceil M/2 \rceil\) 个值,可以从兄弟节点借一个,并更新父节点中的分隔值
- 否则与兄弟节点合并并删除父节点中的分隔值,递归处理父节点
作业题⚓︎
T1:节点数计算
判断:A 2-3 tree with 3 nonleaf nodes must have 18 keys at most.
Answer
T
Tips:叶节点指的是直接连向数值的节点而非数值本体
T2:插入与分裂操作
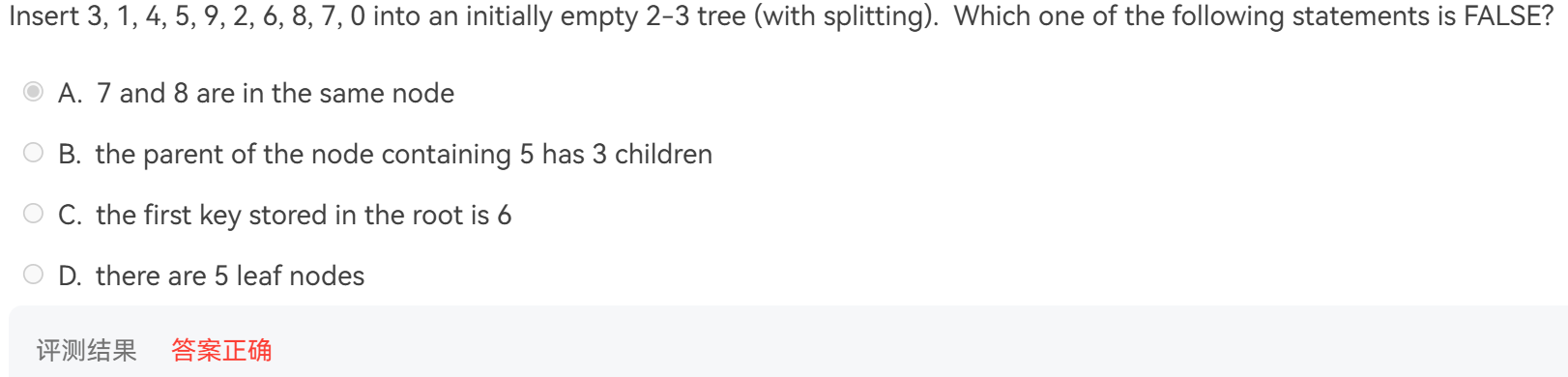
解析
结构大致是(懒得画图,自行意会一下)
[6]
[2,4][8]
[0,1][2,3][4,5][6,7][8,9]
T3:删除操作
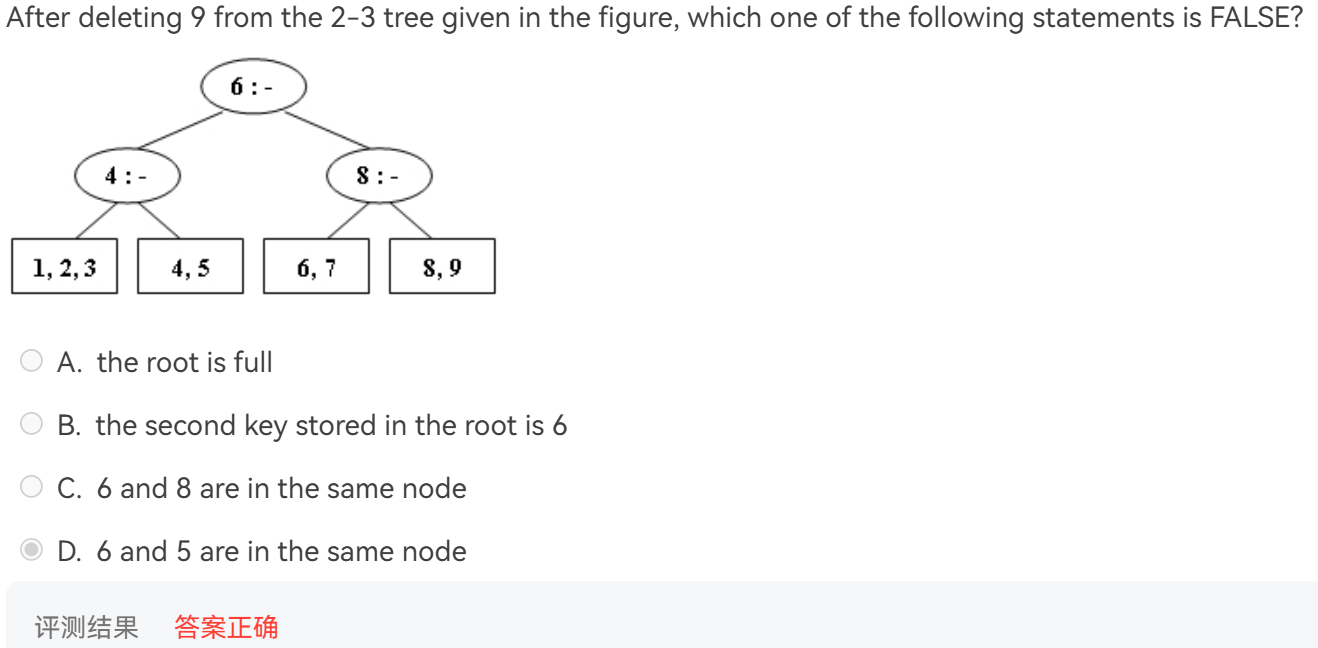
解析
结构是
[4,6]
[1,2,3][4,5][6,7,8]
目前还没有写过删除的代码所以实现细节不明
T4:概念辨析

解析
注意只有根节点这种特例!!