跳转至

Splay⚓︎

概述⚓︎

splay相较于AVL并没有那么严格的平衡维护，而是通过每个操作之后将操作对象 splay 到根这个操作保持均摊 \(O(\log{n})\) 的复杂度。

其中所谓 splay 到根是指通过一系列旋转让当前节点转到根，其中有三种不同的操作方式。

三种情形

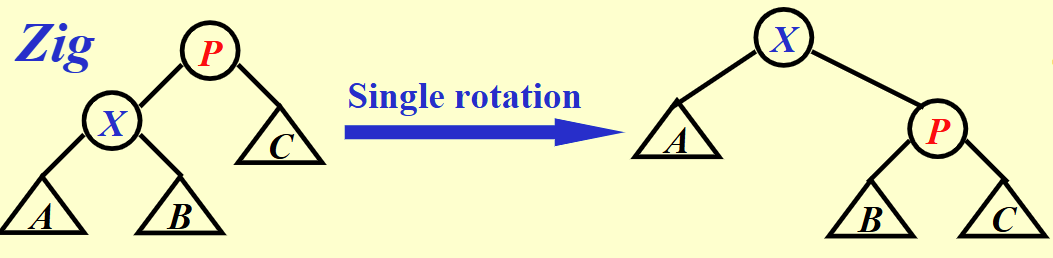
zig : 当前节点向父节点位置旋转

zig

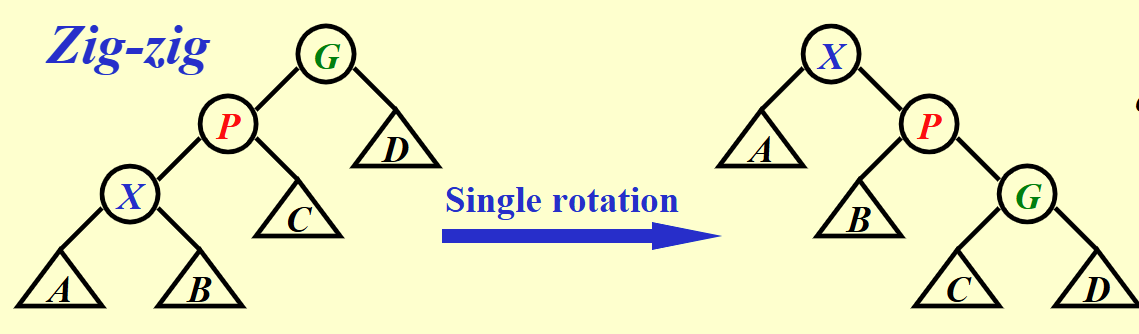
zig-zig : 自己&父节点&再上一级节点方向相同，对 父节点&自己（注意这个顺序）进行同向旋转（我觉得图上应该是 Double rotation ）

zigzig

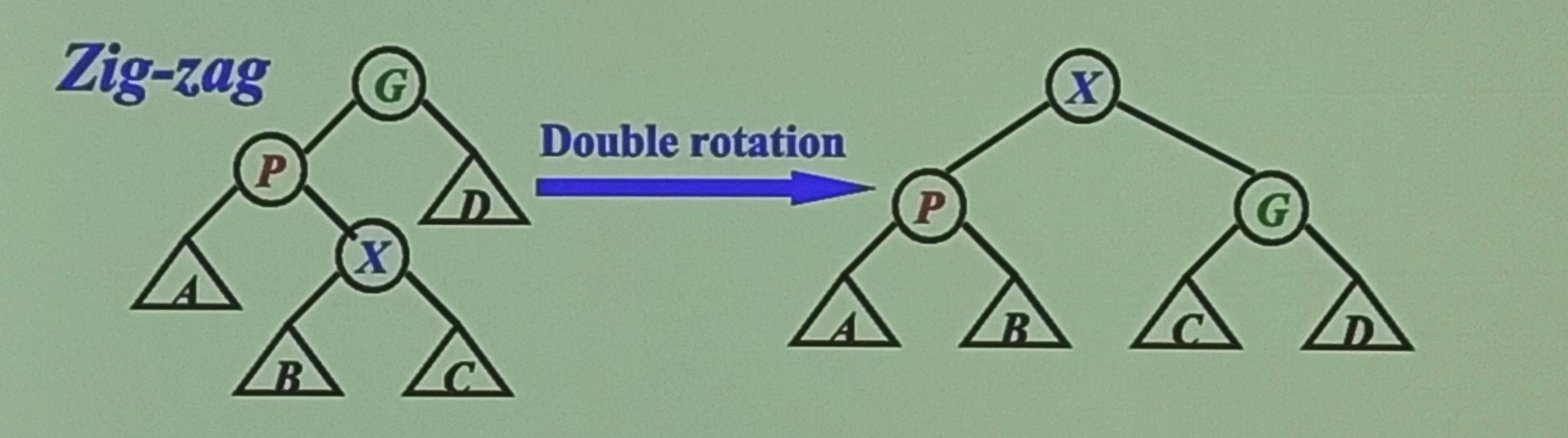
zig-zag : 自己&父节点，父节点&再上一级节点方向不同，对自己进行两次反向旋转

zigzag

Splaying not only moves the accessed node to the root, but also roughly halves the depth of most nodes on the path.

操作⚓︎

Rotate⚓︎

单次旋转与AVL大同小异，但是这里因为存在向上爬的过程需要额外维护父亲关系。在实现上如 AVL 所说将左右旋合并了

Note 
bool get(int x) { return x == ch[fa[x]][1]; }

void Rotate(int x) {
  int y = fa[x], z = fa[y], chk = get(x);
  ch[y][chk] = ch[x][chk ^ 1];
  if (ch[x][chk ^ 1]) fa[ch[x][chk ^ 1]] = y;
  ch[x][chk ^ 1] = y;
  fa[y] = x;
  fa[x] = z;
  if (z) ch[z][y == ch[z][1]] = x;
  maintain(y);
  maintain(x);
}
  • 其中 maintain 只是维护子树信息，由具体使用决定，一般是 \(O(1)\) ， 因而整个操作 \(O(1)\)

Splay⚓︎

旋转方式在开头已经给出，具体而言：

在旋转到深度为1之前每次都要观察父亲和爷爷两个节点并进行 zigzig 或者 zigzag ，最后（可能）进行单次的 zig 。

代码又整合了，相当细节（但是还是那句话，不考）

Code 
bool get(int x) { return x == ch[fa[x]][1]; }
void Splay(int x) {
  for (int f = fa[x]; f = fa[x], f; rotate(x))
    if (fa[f]) Rotate(get(x) == get(f) ? f : x);
  rt = x;
}
  • 复杂度单次可能 \(O(N)\) ，但是均摊是 \(O(\log N)\) 的，分析见 复杂度分析

其他操作⚓︎

相较于 BST 的最大改变就是每次操作都 splay 了，相对来说只有 Delete 操作需要详细说说

  • Find

  • 一路往下找 + splay上去

  • $ O(\log{N})$

  • Delete

  • 找到点并splay上去，如果计数为1则删除节点，否则合并两棵子树，具体而言：

    • 如果有一棵子树为空，则直接保留另一棵子树即可

    • 否则查询当前根节点的前驱（因为包含splay操作，这个前驱此时已经成为根），而要删除的节点此时 必然没有左子树 （因为这个前驱的 splay 最后一步才会影响到待删除节点，它必然和新的根节点是父子关系，另外一方面它也应当是新的根节点的后继），因此只需要并将其右儿子接到根节点上

  • 复杂度 \(O(\log{n})\)

Code

void Delete(int k) { Find(k); if (cnt[rt] > 1) { cnt[rt]--; Maintain(rt); return; } if (!ch[rt][0] && !ch[rt][1]) { Clear(rt); rt = 0; return; } if (!ch[rt][0]) { int cur = rt; rt = ch[rt][1]; fa[rt] = 0; Clear(cur); return; } if (!ch[rt][1]) { int cur = rt; rt = ch[rt][0]; fa[rt] = 0; Clear(cur); return; } int cur = rt, x = Pre(); fa[ch[cur][1]] = x; ch[x][1] = ch[cur][1]; Clear(cur); Maintain(rt); }

  • Insert操作

  • 一路往下找+splay上去

  • \(O(\log{N})\)

Splay操作的复杂度分析⚓︎

写完才发现oiwiki上有很详细的分析...挂个链接

  • 势能函数\(\Phi(p) =\sum_{i\in subtree(p)} \log{S(i)}\)，其中 \(S(i)\) 指 \(i\) 的子树大小。记 \(\log{S(i)} = rank(i)\) ，则 \(\Phi(p)=\sum_{i\in subtree(p)} rank(i)\)

  • zig, zig-zig, zig-zag 操作的复杂度为1,2,2

  • zig :

zig

\[ \begin{aligned} \hat{c_i} =& 1 + \Phi(T_2) - \Phi(T_1)\\ = &1 + R_2(x) - R_1(x) + (R_2(p) - R_1(p))\\ \leq &1 + R_2(x) - R_1(x) \end{aligned} \]
  • zig-zag:

zigzag

\[ \begin{aligned} \hat{c_i} =& 2 + \Phi(T_2) - \Phi(T_1)\\ = &2 + R_2(x) - R_1(x) + R_2(p) - R_1(p) + R_2(g) - R_1(g)\\ \end{aligned} \]

因为\(R_1(g) = R_2(x)\) 故

\[ \begin{aligned} \hat{c_i} = &2 - (R_1(x) + R_1(p) )+ R_2(p) + R_2(g)\\ \leq &2 - 2R_1(x) + R_2(p) + R_2(g) \end{aligned} \]

又因为 $ R_2(p) = \log{(1+A+B)}$, $ R_2(g) = \log{(1+C+D)}$ ，\(R_2(x) = \log(3+A+B+C+D)\)

令 \(a = 1+A+B\) , \(b = 1 + C + D\) , $ c = 3 + A + B + C + D$ , 则 \(a+b\leq c\) ，

\(\log{a}+\log{b} =\log{(ab)}\leq \log{\frac{c^2}{4}} = 2\log{c} - 2\) ， 即

\[ 2+R_2(p)+R_2(g)\leq 2R_2(x) \]

所以

\[ \hat{c_i} \leq 2(R_2(x)-R_1(x)) \]
  • zig-zig :

zigzig

\[ \begin{aligned} \hat{c_i} =& 2 + \Phi(T_2) - \Phi(T_1)\\ = &2 + R_2(x) - R_1(x) + R_2(p) - R_1(p) + R_2(g) - R_1(g)\\ = &2 + R_2(p) + R_2(g) - R_1(p) - R_1(x)\\ \leq &2 + R_2(x) + R_2(g) - 2R_1(x) \end{aligned} \]

同理zig-zag的均值不等式可得$ R_1(x)+R_2(g)-2R_2(x)\leq -2$ ，即 \(2R_2(x) - R_1(x) - R_2(g)\ge 2\)

所以

\[ \begin{aligned} \hat{c_i} \leq &2 + R_2(x) + R_2(g) - 2R_1(x)\leq 3(R_2(x)-R_1(x)) \end{aligned} \]

​ 假设一次splay共计进行了 \(n\) 步，因为单zig只会在转到根出现，则总复杂度 $$ T_n \leq 1+3(R_n(x)-R_0(x)) $$ ​ 而\(R_n(x)\) 为 \(O(\log{n})\)的，所以splay操作也是\(O(\log{n})\)的

​ 值得注意的是\(R_0(x)\)不一定为0

作业题⚓︎

T1:splay(access)操作

T1

Tips:与父亲同向则先转父亲，否则先转自己（然后都要转一次自己）

评论