AVL Trees⚓︎
AVL属于平衡树的一种,通过要求整棵树的平衡性并对其进行维护以保证树高为 \(O(\log{n})\) 的。 在讨论如何保证这个“平衡”之前,先对“平衡”进行定义
定义⚓︎
平衡
- 空树是平衡的
- 非空树是平衡的当且仅当左右子树是平衡的且其高度差不超过1
Balance Factor
\(BF(p) = h_{Lson}-h_{Rson}\)
其中 \(h_p\) 表示以 \(p\) 为根的子树的高度
Note
定义空树高度为 -1 。
在这个定义式中没有绝对值符号,这就意味着 \(BF(p)\) 可以为负数。
对于一棵平衡的数,其根节点的 \(BF\) 的取值只可能为 \(\pm 1\) 或 \(0\) ,而其他情况需要进行调整。
性质⚓︎
- 对于满足要求的平衡树,其树高为 \(O(\log{n})\)
证明
为了构造出极限数据,我们需要尽可能让树变得不平衡,保持每个根节点的 BF 值为 1 是一个简单的方法。
在这一条件下,我们可以轻易得到关于高度为 \(h\) 的树的最小节点数的递推式:
看起来就很斐波那契啊🤔,稍作改写:
这下与斐波那契的形式完全一致了,再考虑一下初值
\(n_0=1\) ,则 \(n_0+1\) 对应于 \(F_3\) ,
那么 \(n_h = F_{h+3}-1\) 。
从斐波那契数列的通项可以看出, \(F_h\) 是 \(h\) 的指数级别,因此 \(h\) 是 \(O(\log{n})\) 的。
实现⚓︎
下面的笔记结合了部分代码,以下是相关的结构体定义
结构体
struct Node{
int lson, rson, val, h;
}t[maxn];
旋转⚓︎
在如何解决非平衡节点方面, AVL 的选择是进行旋转操作,依据 BF 值的正负会有不同的旋转方向及旋转对象,这里先将所有用到的旋转列出来。
最基础的是左旋和右旋,其操作内容可以从这张图看出来
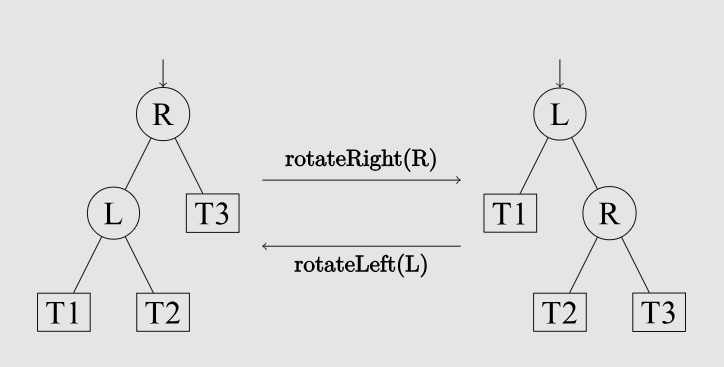
左旋⚓︎
对节点 \(p\) 进行左旋,需要用其右儿子 \(rson\) 替代自己的位置,而 \(p\) 会成为 \(rson\) 的左儿子,这是整个操作的核心目的。
在这个基础上,需要处理 \(rson\) 原本的左子树,将其接到 \(p\) 现在空出来的右子树的位置即可。
Code
int Lrotate(int p){
int rs = t[p].rson;
t[p].rson = t[rs].lson;
t[rs].lson = p;
t[p].h = max(H(t[p].lson),H(t[p].rson))+1;
t[rs].h = max(H(t[rs].lson),H(t[rs].rson))+1;
return rs;
}
右旋⚓︎
右旋的操作与左旋完全对称,将左儿子旋上来,并将其右子树接到 \(p\) 的左子树。
其实如果使用数组表示左右儿子(例如 ch[0] 表示左儿子, ch[1] 表示右儿子),可以通过设置一个参数将左右旋合并为一个参数,此处不详述。
Code
int Rrotate(int p){
int ls = t[p].lson;
t[p].lson = t[ls].rson;
t[ls].rson = p;
t[p].h = max(H(t[p].lson),H(t[p].rson))+1;
t[ls].h = max(H(t[ls].lson),H(t[ls].rson))+1;
return ls;
}
在上述两种旋转的基础上,还有两种复合型的旋转
LR-rotate⚓︎
该操作先将 \(lson\) 进行左旋,再将 \(p\) 进行右旋
Code
int LRrotate(int p){
t[p].lson = Lrotate(t[p].lson);
return Rrotate(p);
}
RL-rotate⚓︎
该操作先将 \(rson\) 右旋再将 \(p\) 左旋
Code
int RLrotate(int p){
t[p].rson = Rrotate(t[p].rson);
return Lrotate(p);
}
操作⚓︎
Maintain⚓︎
参考 oiwiki 的写法,选择将平衡维护这部分单独设计成一个函数。如果没有记错老师PPT中的写法是在其他操作内部嵌入的。由于这部分其实不考代码实现所以无所谓()
下面的配图同样来自 oiwiki ,所以变量名有所不同。
如果某个操作后 D 需要调整,则必然有 \(|BF(D)|=2\) ,以下以左倾为例进行分析,则树的结构如下,右倾只需对称地处理,此处不做赘述。
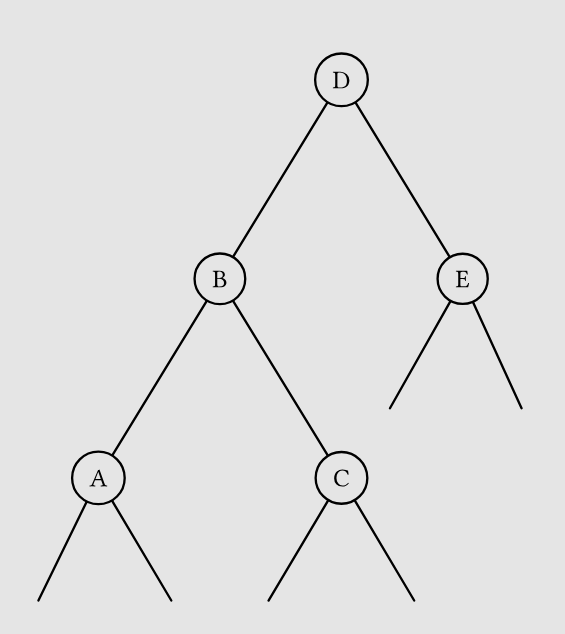
若 \(BF(B)\ge0\) 则先简单 Rrotate(D) ,此时
毫无疑问二者的 BF 值都会减小,那么问题是此时是否合法?
不如想想不合法的条件吧,可能有如下几条,满足一条即可:
由于 \(BF(D) = 2\) 且 \(BF(B)\ge0\) ,我们知道
足以确定旋转后 D 已经平衡,此时情况如下
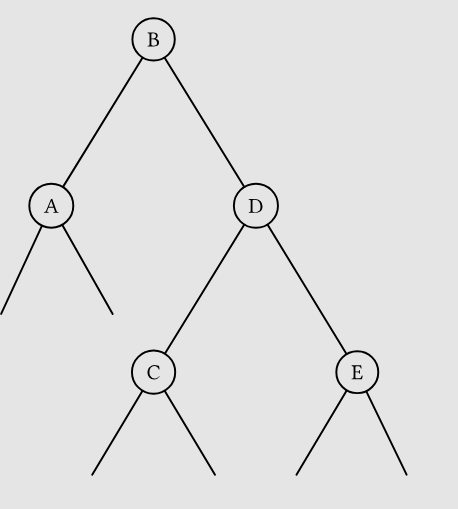
而当 \(BF(B)<0\) 时,情况稍微复杂一些,表明引发不平衡的节点处在左儿子的右子树中,此时进行 LRrotate(D),调整后效果如下 具体分析合法性就摸了我相信老师会分析的而且也不考。
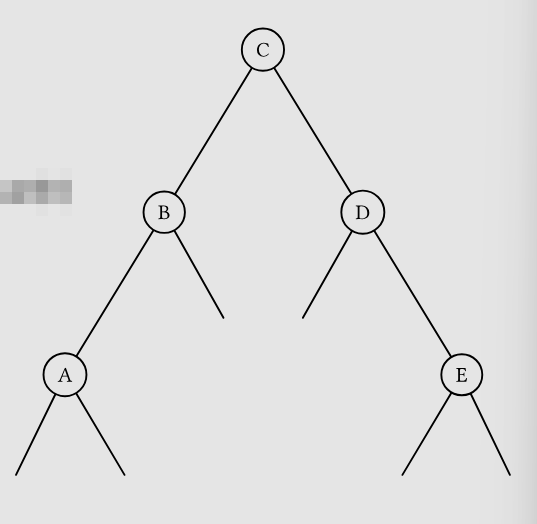
在每个节点处的 maintain 操作复杂度显然 \(O(1)\)。
Code
int H(int p){
return (p <= tot && p != 0)? t[p].h : -1;
}
void Maintain(int p){
int ls = t[p].lson, rs = t[p].rson;
if(H(ls) - H(rs) == 2){
if(H(t[ls].lson) >= H(t[ls].rson)) Rrotate(p);
else LRrotate(p);
}
else if(H(ls) - H(rs) == -2){
if(H(t[rs].rson) >= H(t[rs].lson)) Lrotate(p);
else RLrotate(p);
}
t[p].h = max(H(t[p].lson),H(t[p].rson))+1;
}
Insert⚓︎
首先递归找到需要插入的位置(一个叶节点)并插入, 然后沿着这条递归路径向上更新 BF 值,直到到根节点,并在不平衡节点处进行旋转调整。
- 因为要递归找到叶子所以是 \(O(\log{n})\)
- 只在最近的不平衡祖先进行调整,Maintain 函数中最多进行一次 LR 或者 RL ,因此整个插入过程 Rotate 次数至多为 2
Code
int insert(int p, int v){
if(!p){
t[++tot] = (Node){0, 0, v, 0};
return tot;
}
if(v <= t[p].val) t[p].lson = insert(t[p].lson,v);
else t[p].rson = insert(t[p].rson,v);
Maintain(p);
return p;
}
Delete⚓︎
如果删除一个非叶节点显然会导致整个树型结构崩塌,因此我们需要千方百计地将非叶节点的删除转换为叶节点的删除。(对于一般的平衡树,包括后面的红黑树都是这样处理,但是可以合并的结构是无需考虑这件事的,在学习左偏树和斜堆后应当对此有所了解)
其实转化的方法同堆的删除思路大同小异,即用一个叶子节点来替换本节点。不同的是对于平衡树,删除的节点不一定在根,替换的节点也不是直接从末尾取一个。
具体来说,我们需要找到当前节点的前驱(左儿子一路向右)或者后继(右儿子一路向左),并将该节点与本节点对调值,然后删除。
这样的前驱后继不一定没有儿子,但一定至多一个儿子。对于有儿子的情况直接用儿子顶上来即可。
值得注意的是,删除节点后的向上调整并不停止于第一个失衡的祖先,一个节点删除可能引发上方处于BF值同号临界的一系列祖先都失衡需要旋转,因此旋转次数 \(O(\log{n})\) ,总复杂度 \(O(\log{n})\)
其他的操作都和正常的二叉树一致,不再赘述(应该也不会考),都是 \(O(\log{n})\) 的
作业⚓︎
T1:计算最少节点
If the depth of an AVL tree is 6 (the depth of an empty tree is defined to be -1), then the minimum possible number of nodes in this tree is ___
Answer
33
T2:AVL插入操作
Insert 2, 1, 4, 5, 9, 3, 6, 7 into an initially empty AVL tree. Which one of the following statements is FALSE?
A.4 is the root
B.3 and 7 are siblings
C.2 and 6 are siblings
D.9 is the parent of 7
Answer
B